A spherical planet has uniform density π2×104kg/m3. Find out the minimum period for a satellite in a circular orbit around it in seconds (Use G=203×10−11N−m2kg2).
The correct Answer is:C
To find the minimum period for a satellite in a circular orbit around a spherical planet with uniform density, we can follow these steps:
Step 1: Calculate the Mass of the Planet
The mass M of the planet can be calculated using the formula:
M=ρ⋅V
where ρ is the density and V is the volume of the planet. For a sphere, the volume V is given by:
V=43πR3
Thus, the mass becomes:
M=ρ⋅43πR3
Step 2: Substitute the Density
Given the density ρ=π2×104kg/m3, we substitute this into the mass equation:
M=(π2×104)⋅43πR3
This simplifies to:
M=2π23×104R3
Step 3: Gravitational Force and Centripetal Force
For a satellite in circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force Fg is given by:
Fg=GMmR2
where G is the gravitational constant, m is the mass of the satellite, and R is the radius of the planet.
The centripetal force Fc required for circular motion is:
Fc=mv2R
where v is the orbital speed of the satellite.
Step 4: Equate Gravitational Force and Centripetal Force
Setting the gravitational force equal to the centripetal force:
GMmR2=mv2R
We can cancel m from both sides (assuming m≠0):
GMR2=v2R
This simplifies to:
v2=GMR
Step 5: Substitute for Mass M
Substituting the expression for M:
v2=G(2π23×104R3)R
This simplifies to:
v2=2π23×104R2G
Step 6: Calculate the Period
The orbital period T is related to the speed v and the radius R by:
T=2πRv
Substituting v:
T=2πR√2π23×104R2G
This simplifies to:
T=2πR√2π23×104G⋅R
T=2π√2π23×104G
Step 7: Substitute Values
Now substituting G=203×10−11N m2/kg2:
T=2π√2π23×104×203×10−11
Calculating this gives:
T=2π√40π29×10−7
T=2π2π3×10−3.5=3×103 seconds
Final Answer
Thus, the minimum period for the satellite in a circular orbit around the planet is:
T≈3000 seconds
The mass M of the planet can be calculated using the formula:
M=ρ⋅V
where ρ is the density and V is the volume of the planet. For a sphere, the volume V is given by:
V=43πR3
Thus, the mass becomes:
M=ρ⋅43πR3
Given the density ρ=π2×104kg/m3, we substitute this into the mass equation:
M=(π2×104)⋅43πR3
This simplifies to:
M=2π23×104R3
For a satellite in circular orbit, the gravitational force provides the necessary centripetal force. The gravitational force Fg is given by:
Fg=GMmR2
where G is the gravitational constant, m is the mass of the satellite, and R is the radius of the planet.
Fc=mv2R
where v is the orbital speed of the satellite.
Setting the gravitational force equal to the centripetal force:
GMmR2=mv2R
We can cancel m from both sides (assuming m≠0):
GMR2=v2R
This simplifies to:
v2=GMR
Substituting the expression for M:
v2=G(2π23×104R3)R
This simplifies to:
v2=2π23×104R2G
The orbital period T is related to the speed v and the radius R by:
T=2πRv
Substituting v:
T=2πR√2π23×104R2G
This simplifies to:
T=2πR√2π23×104G⋅R
T=2π√2π23×104G
Now substituting G=203×10−11N m2/kg2:
T=2π√2π23×104×203×10−11
Calculating this gives:
T=2π√40π29×10−7
T=2π2π3×10−3.5=3×103 seconds
Thus, the minimum period for the satellite in a circular orbit around the planet is:
T≈3000 seconds
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Main (Archive)
Explore 43 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:LEVEL -0 Long Answer Type
Explore 3 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
A rod of 1.5m length and uniform density 104kg/m3 is rotating at an angular velocity 400rad/sec about its one end in a horizontal plane. Find out elongation in rod.
Given y=2×1011N/m2
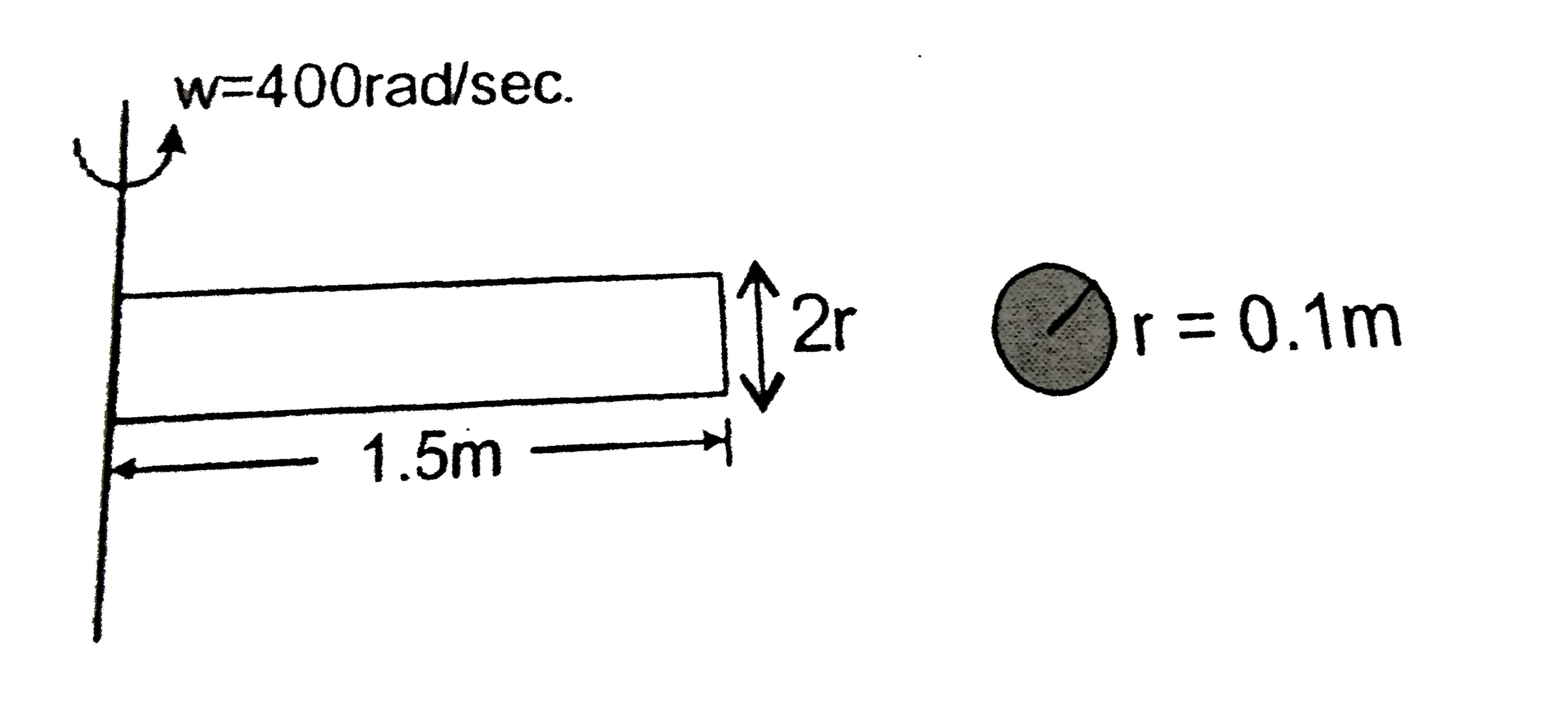
View SolutionTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
View SolutionThe mass of planet Jupiter is 1.9×107kg and that of the Sun is 1.99×1030kg. The mean distance of Jupiter from the Sun is 7.8×1011m. Calculate the gravitational force which Sun exerts on Jupiter. Assuming that Jupiter moves in circular orbit around the Sun, also calculate the speed of Jupiter G=6.67×10−11Nm2kg−2.
View SolutionGiven Y=2×1011N/m2,ρ=104kg/m3
Find out elongation in rod.

View SolutionYoungs modulus of a string of length 1m and Density 900Kgm3 is 9×109Nm2. Find the minimum reasonance frequency in (Hz) can be produced in the string if strain in the string is 4.9×10−4.
View SolutionA planet has a mass of 2.4×1026 kg with a diameter of 3×108 m. What will be the acceleration due to gravity on that planet ?
View SolutionA stress of 106N/m2 is required for breaking a material. If the density of the material is 3×103Kg/m3, then what should be the minimum length of the wire made of the same material so that it breaks by its own weight (g=10m/s2)
View SolutionA hemispherical bowl just floats without sinking in a liquid of density 1.2×103kg/m3. If outer diameter and the density of the bowl are 1m and 2×104kg/m3 respectively, then the inner diameter of bowl will be
View SolutionA hemispherical bowl just floats without sinking in a liquid of density 1.2×103kg/m3. If outer diameter and the density of the bowl are 1m and 2×104kg/m3 respectively, then the inner diameter of bowl will be
View SolutionA substance breaks down under a stress of 105 Pa. If the density of the substance is 2×103kgm3, find the minimum length of the wire made of this substance which will break under its own weight (g=10ms2)
View Solution