A planet of mass m is the elliptical orbit about the sun (m<<Msun) with an orbital period T. If A be the area of orbit, then its angular momentum would be:
2mAT
mAT
mA2T
2mAT
The correct Answer is:A
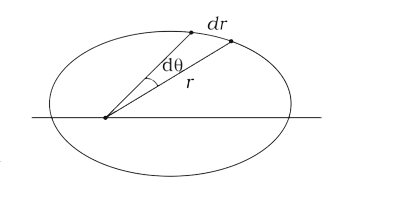
Area of the triangle shown is dA=12r×dr
⇒dA=12×r×rdθ=r22dθ
Dividing both side by dt ,
dAdt=r22dθdt=r22ω=mr2ω2m=Iω2m=L2m⇒dA=L2mdt
Integrating both sides, we get ⇒A=L2m×T⇒L=2mAT
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Main (Archive)
Explore 43 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:LEVEL -0 Long Answer Type
Explore 3 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
Knowledge Check
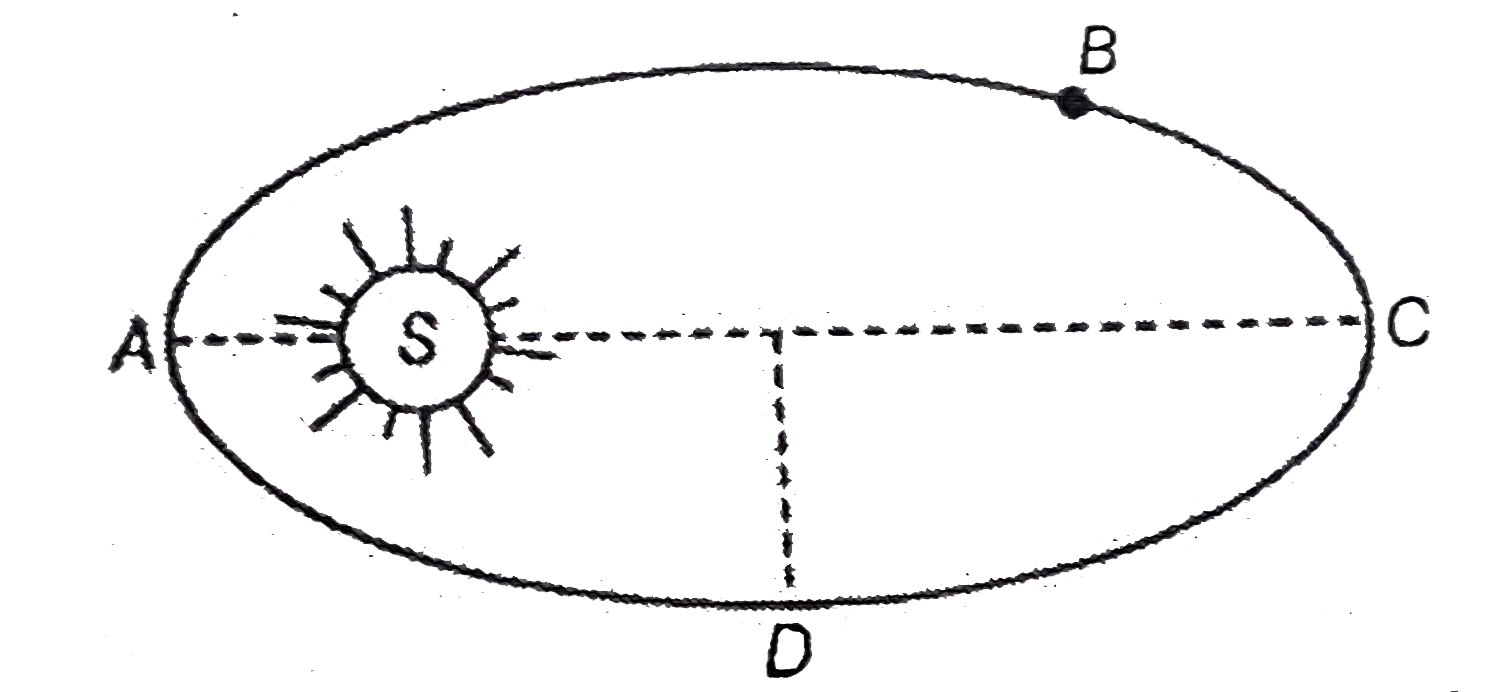
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 AABBCCDD
AABBCCDDA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
The orbital with zero orbital angular momentum is.
View SolutionA planet of mass m is moving in an elliptical orbit about the sun (mass of sun = M). The maximum and minimum distances of the planet from the sun are r1 and r2 respectively. The period of revolution of the planet wil be proportional to :
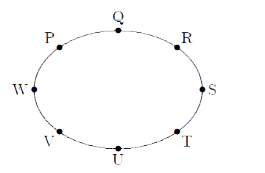
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
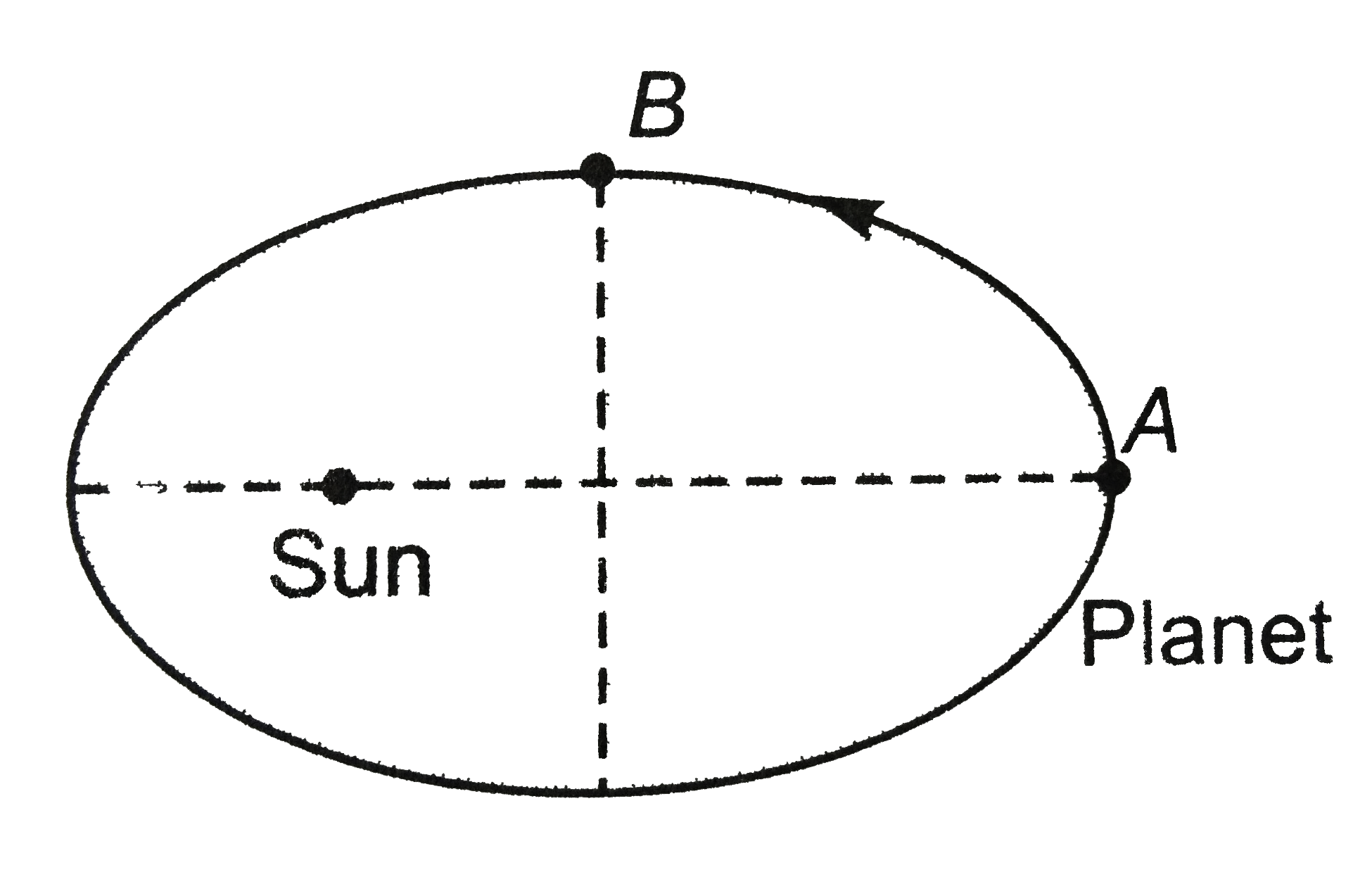
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View Solution