A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing is 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
(a)4.7 rad/s
(b)9.8 rad/s
(c)24 rad/s
(d)1 rad/s
The correct Answer is:A
To solve the problem, we need to find the minimum rotational speed of the cylindrical drum so that the man does not fall when the floor is suddenly removed. We will use the concepts of circular motion and friction.
1. Identify the Forces Acting on the Man:
- The man experiences two main forces:
- The gravitational force acting downwards: Fg=mg
- The normal force acting perpendicular to the wall of the cylinder: Fn
2. Frictional Force:
- The frictional force that prevents the man from sliding down is given by:
Ff=μFn
- Where μ is the coefficient of friction.
3. Centripetal Force Requirement:
- For the man to remain in circular motion against the wall, the normal force must provide the necessary centripetal force:
Fn=mv2r
- Where v is the tangential speed and r is the radius of the cylinder.
4. Relate Tangential Speed to Angular Velocity:
- The relationship between tangential speed v and angular velocity ω is:
v=rω
- Substituting this into the centripetal force equation gives:
Fn=m(rω)2r=mrω2
5. Setting Up the Equations:
- The frictional force must balance the gravitational force for the man to not fall:
Ff=Fg
- Therefore:
μFn=mg
- Substituting Fn:
μ(mrω2)=mg
6. Solving for Angular Velocity ω:
- We can simplify the equation:
μmrω2=mg
- Dividing both sides by m:
μrω2=g
- Rearranging gives:
ω2=gμr
- Taking the square root:
ω=√gμr
7. Substituting Known Values:
- Given:
- g=10m/s2 (approximating)
- μ=0.15
- r=3m
- Substitute these values into the equation:
ω=√100.15×3=√100.45=√22.22≈4.72rad/s
Final Answer:
The minimum rotational speed of the cylinder is approximately ω≈4.72rad/s.
---
- The man experiences two main forces:
- The gravitational force acting downwards: Fg=mg
- The normal force acting perpendicular to the wall of the cylinder: Fn
- The frictional force that prevents the man from sliding down is given by:
Ff=μFn
- Where μ is the coefficient of friction.
- For the man to remain in circular motion against the wall, the normal force must provide the necessary centripetal force:
Fn=mv2r
- Where v is the tangential speed and r is the radius of the cylinder.
- The relationship between tangential speed v and angular velocity ω is:
v=rω
- Substituting this into the centripetal force equation gives:
Fn=m(rω)2r=mrω2
- The frictional force must balance the gravitational force for the man to not fall:
Ff=Fg
- Therefore:
μFn=mg
- Substituting Fn:
μ(mrω2)=mg
- We can simplify the equation:
μmrω2=mg
- Dividing both sides by m:
μrω2=g
- Rearranging gives:
ω2=gμr
- Taking the square root:
ω=√gμr
- Given:
- g=10m/s2 (approximating)
- μ=0.15
- r=3m
- Substitute these values into the equation:
ω=√100.15×3=√100.45=√22.22≈4.72rad/s
The minimum rotational speed of the cylinder is approximately ω≈4.72rad/s.
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2
49 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
4 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
A 70 kg man stands in contact against the wall of a cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15 m What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View SolutionA block of mass 10 kg in contact against the inner wall of a hollow cylindrical drum of radius 1m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be (g=10m/s2)
View SolutionA block is mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. the frictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
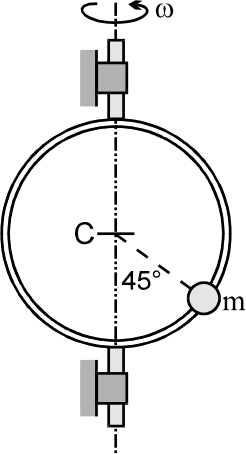
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
View SolutionA 70 kg man standing on ice throws a 3 kg body horizontally at 8m//s. The friction coefficient between the ice and his feet is 0.02. The distance, the man slip is
View SolutionTwo bodies A and B of masses 5 kg and 10 kg in contact with each other rest on a table against a rigid wall as shown in fig. The coefficient of friction between the bodies and the table is 0.15. A force 200 N is applied horizontally to A. What are
(a) the reaction of the partition
(b) the action-reaction forces between A and B ?
(c) What happens when the wall is removed? Does the answer to (b) change, when the bodies are in motion? Ignore the difference between μs and μk
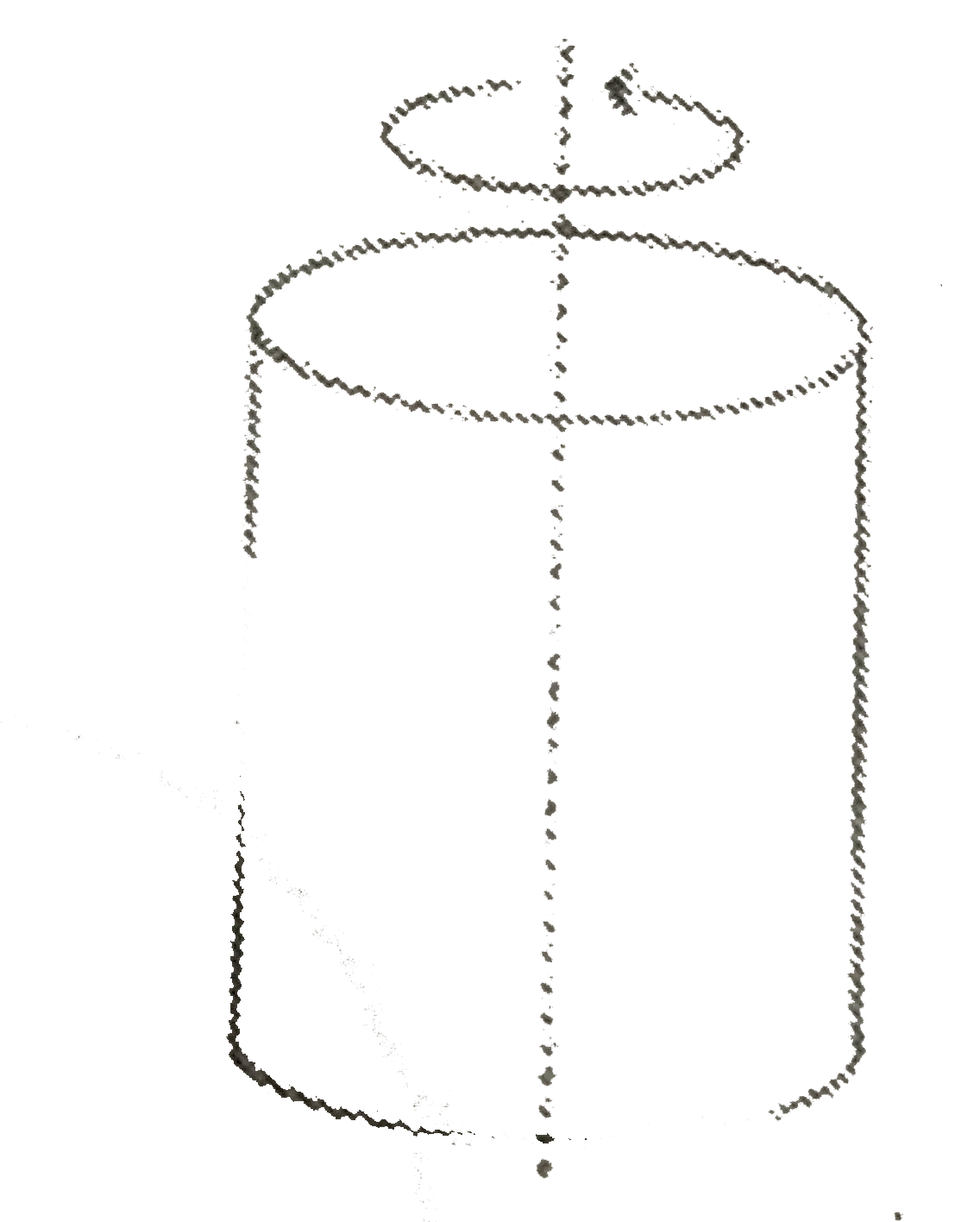
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity ω about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View Solution
