At what angle with the horizontal should a ball be thrown so that the range R is related to the time of flight as R=5T2 ? (Takeg=10ms6−2).
(a)30∘
(b)45∘
(c)60∘
(d)90∘
The correct Answer is:B
To solve the problem of finding the angle at which a ball should be thrown so that the range R is related to the time of flight T as R=5T2, we can follow these steps:
Step 1: Understand the relationship between range and time of flight
The range R of a projectile is given by the formula:
R=V2sin2θg
where V is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
The time of flight T for a projectile is given by:
T=2Vsinθg
Step 2: Express R in terms of T
From the problem, we have:
R=5T2
We can substitute T from the time of flight formula into this equation. First, we solve for T:
T=2Vsinθg
Now, substituting T into R=5T2:
R=5(2Vsinθg)2
This simplifies to:
R=5⋅4V2sin2θg2=20V2sin2θg2
Step 3: Set the two expressions for R equal
Now we have two expressions for R:
1. R=V2sin2θg
2. R=20V2sin2θg2
Setting them equal to each other:
V2sin2θg=20V2sin2θg2
Step 4: Simplify the equation
We can cancel V2 from both sides (assuming V≠0):
sin2θg=20sin2θg2
Multiplying both sides by g2:
gsin2θ=20sin2θ
Step 5: Use the identity for sin2θ
Using the identity sin2θ=2sinθcosθ:
g(2sinθcosθ)=20sin2θ
Substituting g=10m/s2:
10(2sinθcosθ)=20sin2θ
This simplifies to:
20sinθcosθ=20sin2θ
Dividing both sides by 20:
sinθcosθ=sin2θ
Step 6: Rearranging the equation
Rearranging gives:
sinθcosθ−sin2θ=0
Factoring out sinθ:
sinθ(cosθ−sinθ)=0
Step 7: Solving for θ
This gives us two cases:
1. sinθ=0 (which corresponds to θ=0∘ or 180∘, not valid for projectile motion)
2. cosθ−sinθ=0 which leads to cosθ=sinθ
This implies:
tanθ=1
Thus, θ=45∘.
Conclusion
The angle at which the ball should be thrown is θ=45∘.
---
The range R of a projectile is given by the formula:
R=V2sin2θg
where V is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
T=2Vsinθg
From the problem, we have:
R=5T2
We can substitute T from the time of flight formula into this equation. First, we solve for T:
T=2Vsinθg
Now, substituting T into R=5T2:
R=5(2Vsinθg)2
This simplifies to:
R=5⋅4V2sin2θg2=20V2sin2θg2
Now we have two expressions for R:
1. R=V2sin2θg
2. R=20V2sin2θg2
V2sin2θg=20V2sin2θg2
We can cancel V2 from both sides (assuming V≠0):
sin2θg=20sin2θg2
Multiplying both sides by g2:
gsin2θ=20sin2θ
Using the identity sin2θ=2sinθcosθ:
g(2sinθcosθ)=20sin2θ
Substituting g=10m/s2:
10(2sinθcosθ)=20sin2θ
This simplifies to:
20sinθcosθ=20sin2θ
Dividing both sides by 20:
sinθcosθ=sin2θ
Rearranging gives:
sinθcosθ−sin2θ=0
Factoring out sinθ:
sinθ(cosθ−sinθ)=0
This gives us two cases:
1. sinθ=0 (which corresponds to θ=0∘ or 180∘, not valid for projectile motion)
2. cosθ−sinθ=0 which leads to cosθ=sinθ
tanθ=1
Thus, θ=45∘.
The angle at which the ball should be thrown is θ=45∘.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionA fighter plane is flying horizontally at an altitude of 1.5 km with speed 720kmh−1. At what angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? (Takeg=10ms−2)
View SolutionA particle is projected from the ground with velocity u at angle θ with horizontal. The horizontal range, maximum height and time of flight are R,H and T respectively. They are given by, R=u2sin2θg,H=u2sin2θ2g and T=2usinθg Now keeping u as fixed, θ is varied from 30∘ to 60∘. Then,
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
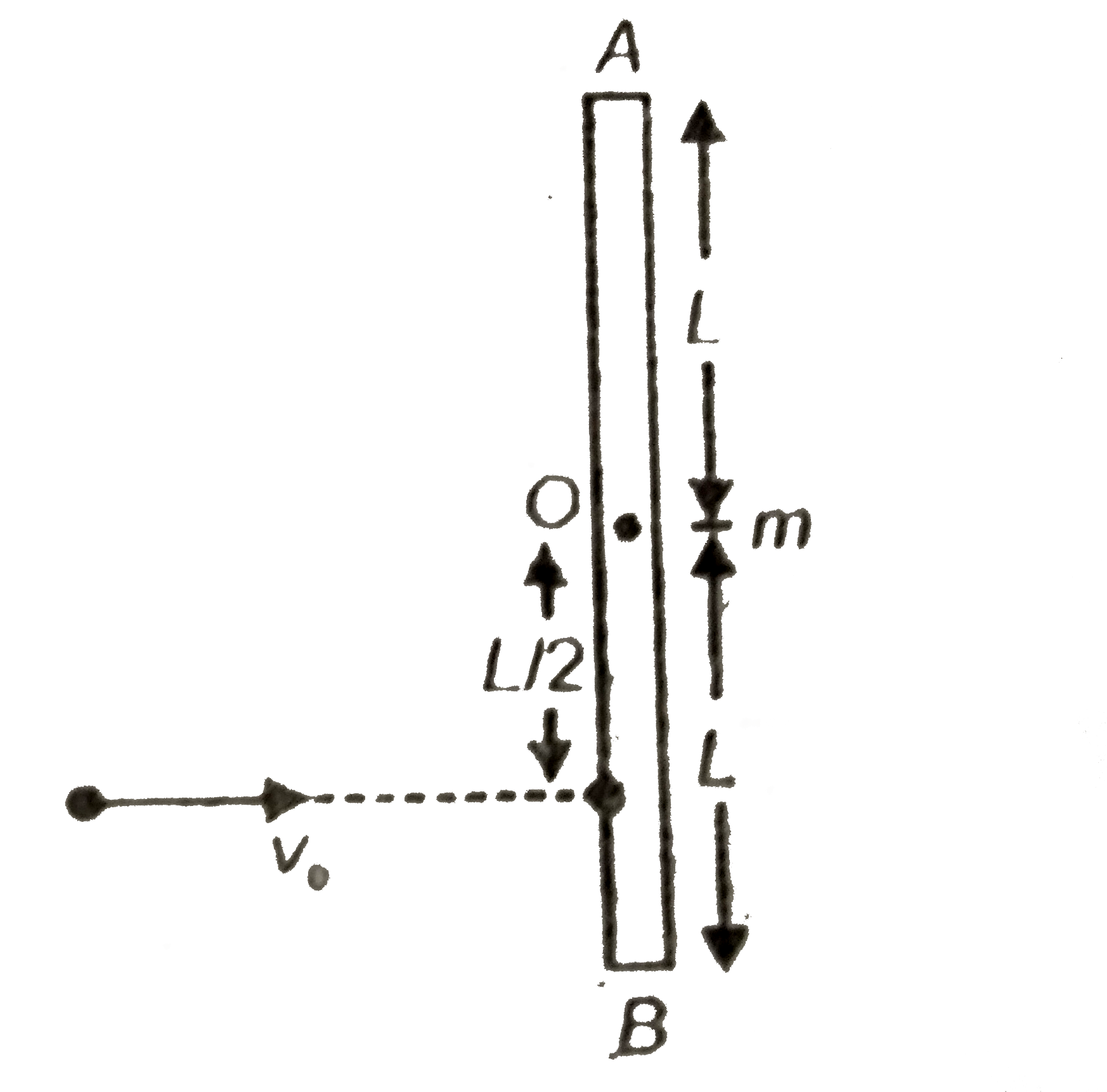
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionA particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
View SolutionA ball is thrown at a speed of 40 m/s at an angle of 600 with the horizontal. Find a. the maximum height reached and b. the range of te ball. Take g=10ms2.
View SolutionThe ceiling of a tunnel is 5 m high. What is the maximum horizontal distance that a ball thrown with a speed of 20ms−1 can go without hitting the ceiling of the tunnel (g=10ms−2)
View SolutionTwo projectiles A and B are projected with same speed at an angle 30∘ and 60∘ to the horizontal, then which of the following is not valid where T is total time of flight, H is max height and R is horizontal range.
View SolutionA ball is thrown upwards from the ground with an initial speed of u. The ball is at height of 80m at two times, the time interval being 6 s. Find u. Take g=10m/s2.
View Solution

