The stopping potential for photoelectrons from a metal surface is V1 when monochromatic light of frequency υ1 is incident on it. The stopping potential becomes V2 when monochromatic light of another frequency is incident on the same metal surface. If h be the Planck’s constant and e be the charge of an electron, then the frequency of light in the second case is:
(a)υ1−eh(V2+V1)
(b)υ1+eh(V2+V1)
(c)υ1−eh(V2−V1)
(d)υ1+eh(V2−V1)
The correct Answer is:D
To solve the problem, we will use the photoelectric effect equation and the concept of stopping potential. The stopping potential is related to the kinetic energy of the emitted photoelectrons.
1. Understanding the Photoelectric Effect:
The photoelectric effect is described by the equation:
K.E.=hν−ϕ
where K.E. is the kinetic energy of the emitted electrons, h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
2. Relating Stopping Potential to Kinetic Energy:
The stopping potential V is related to the kinetic energy by:
K.E.=eV
where e is the charge of an electron. Therefore, we can write:
eV1=hν1−ϕ(1)
for the first frequency ν1 and stopping potential V1.
3. Setting Up the Equation for the Second Frequency:
Similarly, for the second frequency ν2 and stopping potential V2:
eV2=hν2−ϕ(2)
4. Subtracting the Two Equations:
Now, we can subtract equation (1) from equation (2):
eV2−eV1=(hν2−ϕ)−(hν1−ϕ)
This simplifies to:
e(V2−V1)=h(ν2−ν1)
5. Solving for the Frequency ν2:
Rearranging the equation gives:
hν2=e(V2−V1)+hν1
Dividing by h:
ν2=e(V2−V1)h+ν1
6. Final Expression:
Thus, the frequency of light in the second case is:
ν2=ν1+e(V2−V1)h
The photoelectric effect is described by the equation:
K.E.=hν−ϕ
where K.E. is the kinetic energy of the emitted electrons, h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
The stopping potential V is related to the kinetic energy by:
K.E.=eV
where e is the charge of an electron. Therefore, we can write:
eV1=hν1−ϕ(1)
for the first frequency ν1 and stopping potential V1.
Similarly, for the second frequency ν2 and stopping potential V2:
eV2=hν2−ϕ(2)
Now, we can subtract equation (1) from equation (2):
eV2−eV1=(hν2−ϕ)−(hν1−ϕ)
This simplifies to:
e(V2−V1)=h(ν2−ν1)
Rearranging the equation gives:
hν2=e(V2−V1)+hν1
Dividing by h:
ν2=e(V2−V1)h+ν1
Thus, the frequency of light in the second case is:
ν2=ν1+e(V2−V1)h
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 18Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 18Exercise:PHYSICS - SECTION 2
Explore 5 Videos
- JEE MAIN REVISION TEST - 13Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 13Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 19Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 19Exercise:PHYSICS
Explore 25 Videos
Similar Questions
If the frequency of incident light is tripled, the stopping potential will
View SolutionWhen light of wavelength λ is incident on a metal surface ,stopping potential is found to be V∘ . When light of wavelength nλ is in incident on the same metal surface ,stopping potential is found to be V∘n+1. The threshold wavelength of the metal is
View Solution
Knowledge Check
A metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
AV1+he(v1+v2)BV1+he(v1−v2)CV1+eh(v2−v1)DV1−he(v1+v2)A metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
AV1+he(v1+v2)BV1+he(v2−v1)CV1+eh(v2−v1)DV1−he(v1+v2)
The slope of frequency of incident light and stopping potential for a given surface will be
View SolutionWhen light of wavelength λ is incident on a metal surface, stopping potential is found to be x. When light of wavelength nλ is incident on the same metal surface, stopping potential is found to be xn+1 . Find the threshold wavelength of the metal.
View SolutionMonochromatic light of wavelength 198 nm is incident on the surface of a metal, whose work function is 2.5 eV. Calculate the stopping potential.
View SolutionThe stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
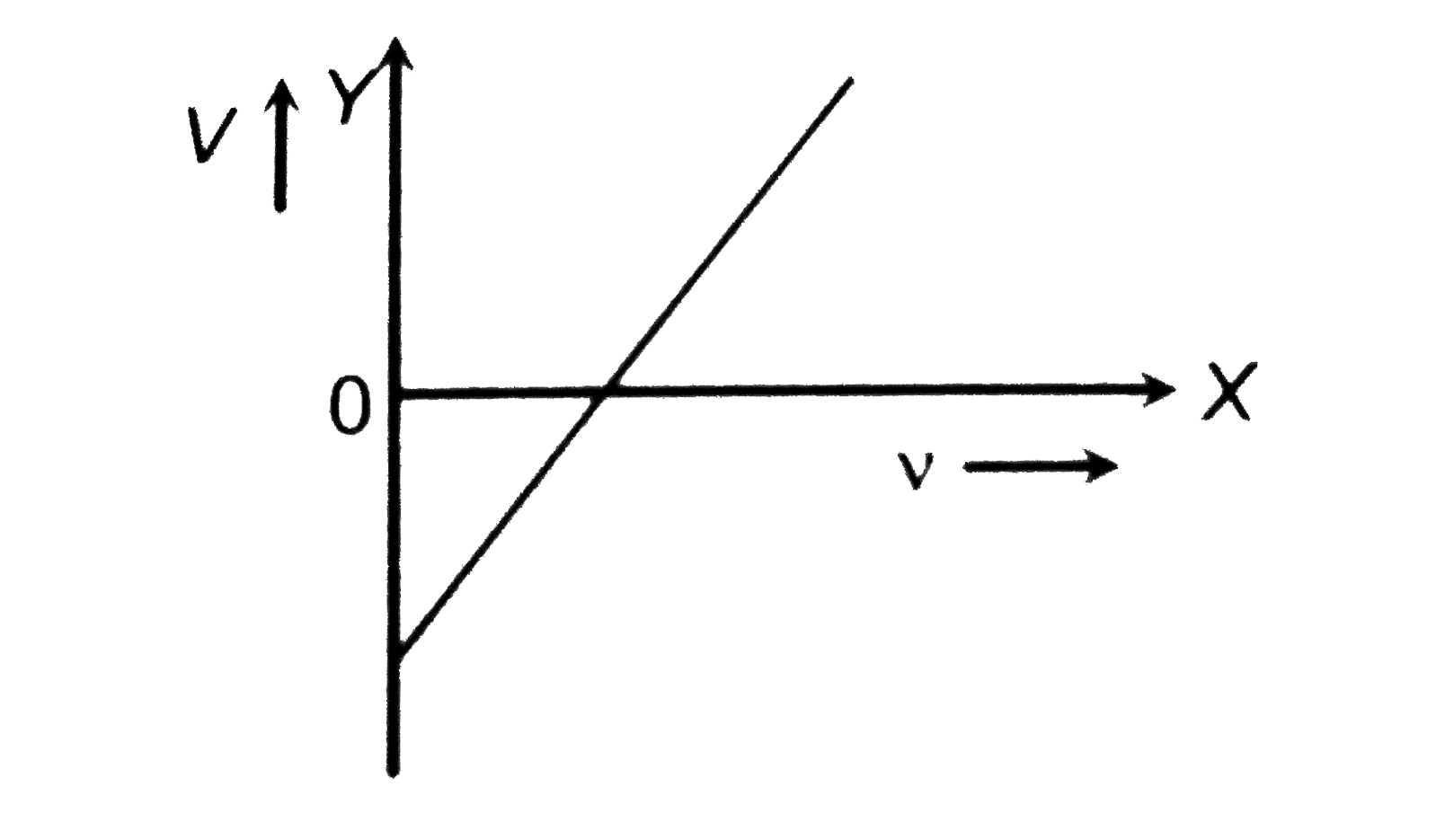
View Solution
The stopping potential V for photoelectric emission from a metal surface is plotted along Y - axis and frequency v of incident light along X - axis . A straight line is obtained as shown . Planck's constant is given by
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght λ1=550nm is incident on it. The stopping potential for such electrons is λS1=0.19V. Suppose that radiation of wavelength λ2=190nm is incident of the surface.
Q. Calculate the stopping potential VS2.
View Solution