If the frequency of incident light is tripled, the stopping potential will
be tripled
become one third
become more than triple
become less than triple but more than double
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the frequency of incident light and the stopping potential in the context of the photoelectric effect.
1. Understanding the Photoelectric Effect:
The photoelectric effect states that when light of a certain frequency (ν) shines on a metal surface, it can eject electrons from that surface. The kinetic energy (KE) of the emitted electrons is given by the equation:
KE=hν−ϕ
where h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
2. Relating Kinetic Energy to Stopping Potential:
The kinetic energy of the emitted electrons can also be expressed in terms of the stopping potential (Vs):
KE=eVs
where e is the charge of the electron and Vs is the stopping potential.
3. Setting the Equations Equal:
Since both expressions represent the kinetic energy of the emitted electrons, we can set them equal to each other:
eVs=hν−ϕ
4. Expressing Stopping Potential:
Rearranging the equation gives us the stopping potential in terms of frequency:
Vs=hν−ϕe
5. Effect of Tripling the Frequency:
If the frequency of the incident light is tripled (i.e., ν becomes 3ν), we can substitute this into our equation for stopping potential:
V′s=h(3ν)−ϕe
Simplifying this gives:
V′s=3hν−ϕe
6. Comparing the New Stopping Potential to the Original:
The original stopping potential was:
Vs=hν−ϕe
If we compare V′s to Vs:
V′s=3(hν−ϕe)+(additional term due to the work function)
Since the work function ϕ remains constant, the stopping potential will increase proportionally to the increase in frequency.
7. Conclusion:
Therefore, if the frequency of the incident light is tripled, the stopping potential will also be tripled:
V′s=3Vs
Final Answer:
The stopping potential will be tripled.
---
The photoelectric effect states that when light of a certain frequency (ν) shines on a metal surface, it can eject electrons from that surface. The kinetic energy (KE) of the emitted electrons is given by the equation:
KE=hν−ϕ
where h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
The kinetic energy of the emitted electrons can also be expressed in terms of the stopping potential (Vs):
KE=eVs
where e is the charge of the electron and Vs is the stopping potential.
Since both expressions represent the kinetic energy of the emitted electrons, we can set them equal to each other:
eVs=hν−ϕ
Rearranging the equation gives us the stopping potential in terms of frequency:
Vs=hν−ϕe
If the frequency of the incident light is tripled (i.e., ν becomes 3ν), we can substitute this into our equation for stopping potential:
V′s=h(3ν)−ϕe
Simplifying this gives:
V′s=3hν−ϕe
The original stopping potential was:
Vs=hν−ϕe
If we compare V′s to Vs:
V′s=3(hν−ϕe)+(additional term due to the work function)
Since the work function ϕ remains constant, the stopping potential will increase proportionally to the increase in frequency.
Therefore, if the frequency of the incident light is tripled, the stopping potential will also be tripled:
V′s=3Vs
The stopping potential will be tripled.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE-I ASSERTION AND REASON
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE=II
42 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
Similar Questions
Assertion: If frequency of incident light is doubled, the stopping potential will also become two times
Reason: Stopping potential is given by V0=he(v−v0)
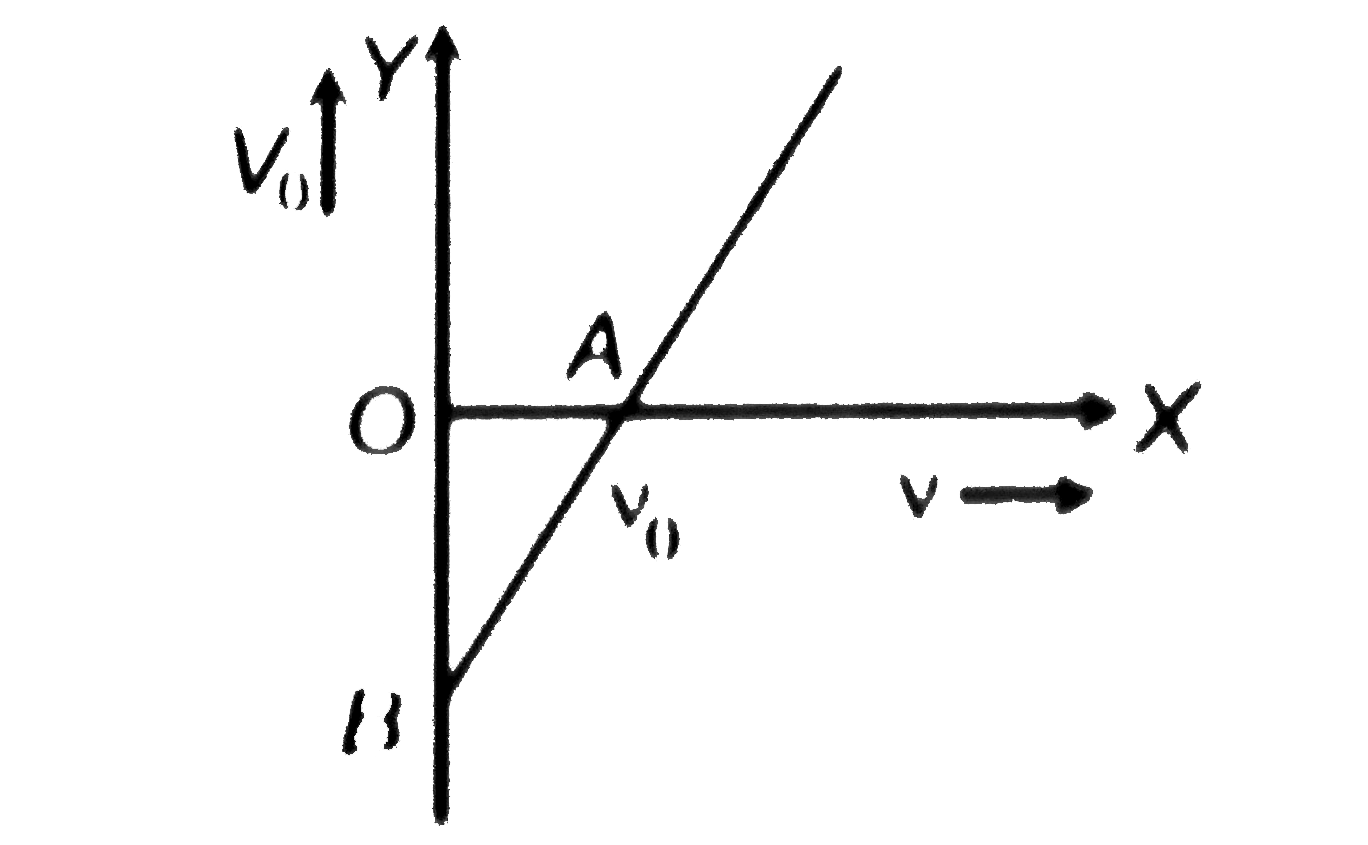
View SolutionIn an experiment on photoelectric effect the frequency f of the incident light is plotted against the stopping potential V0. The work function of the photoelectric surface is given by ( e is the electronic charge)
View Solution
Knowledge Check
Assertion : The stopping potential depends on the frequency of incident light.
Reason : The stopping potential is related to maximum kinetic energy by eV0=Kmax.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.In a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
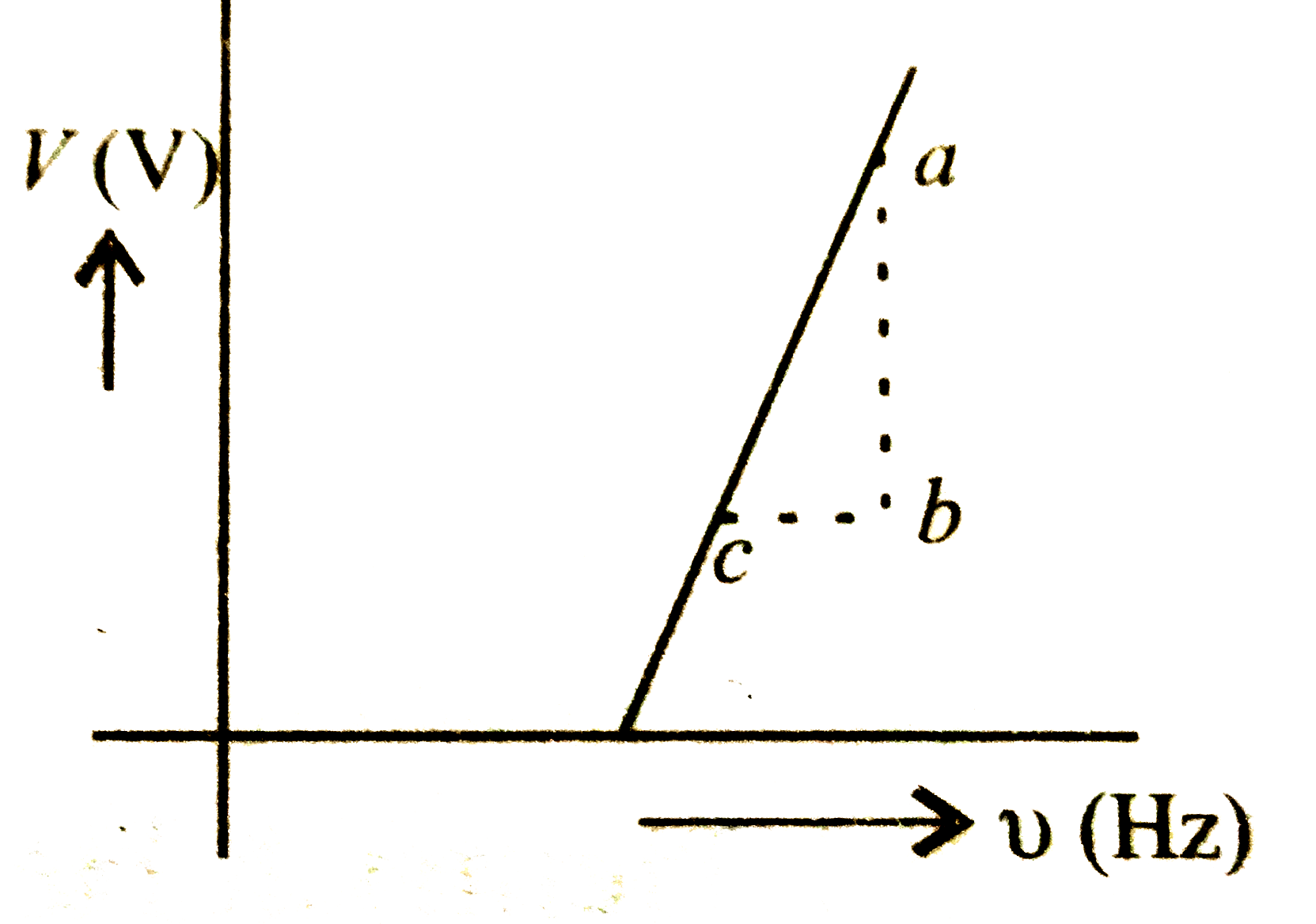 AeabbcBecbacCeacbcDeacab
AeabbcBecbacCeacbcDeacabThe work function of Cs is 2.14 ev find the wavelength of the incident light if the stopping potential is 0.6 V.
A326 nmB454 nmC524 nmD232 nm
The slope of frequency of incident light and stopping potential for a given surface will be
View SolutionAssertion: Stopping potential depends upon the frequency of incident light but is independent of the intensity of the light.
Reason :The maximum kinetic energy of the photoclectrons is proportional to stopping potential
View SolutionThe graph between frequency of incident radiations and stopping potential for a given photosensitive material as follows.
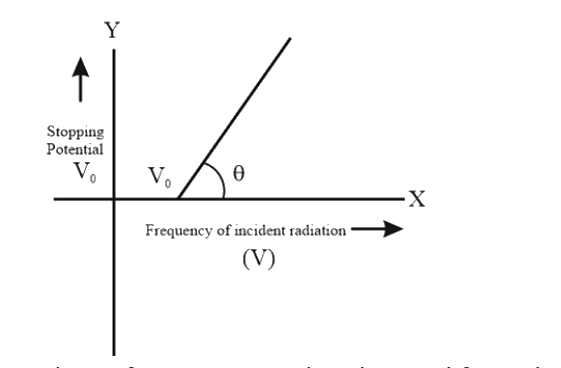
What information can be obtained from the value of the intercept on the potential axis ?
View SolutionIn the previous question, if the intensity of light is made 4I0, then the stopping potential will become
View SolutionA metallic surface is irradiated by a monochromatic light of frequency v1 and stopping potential is found to be V1. If the light of frequency v2 irradiates the surface, the stopping potential will be
View Solution
