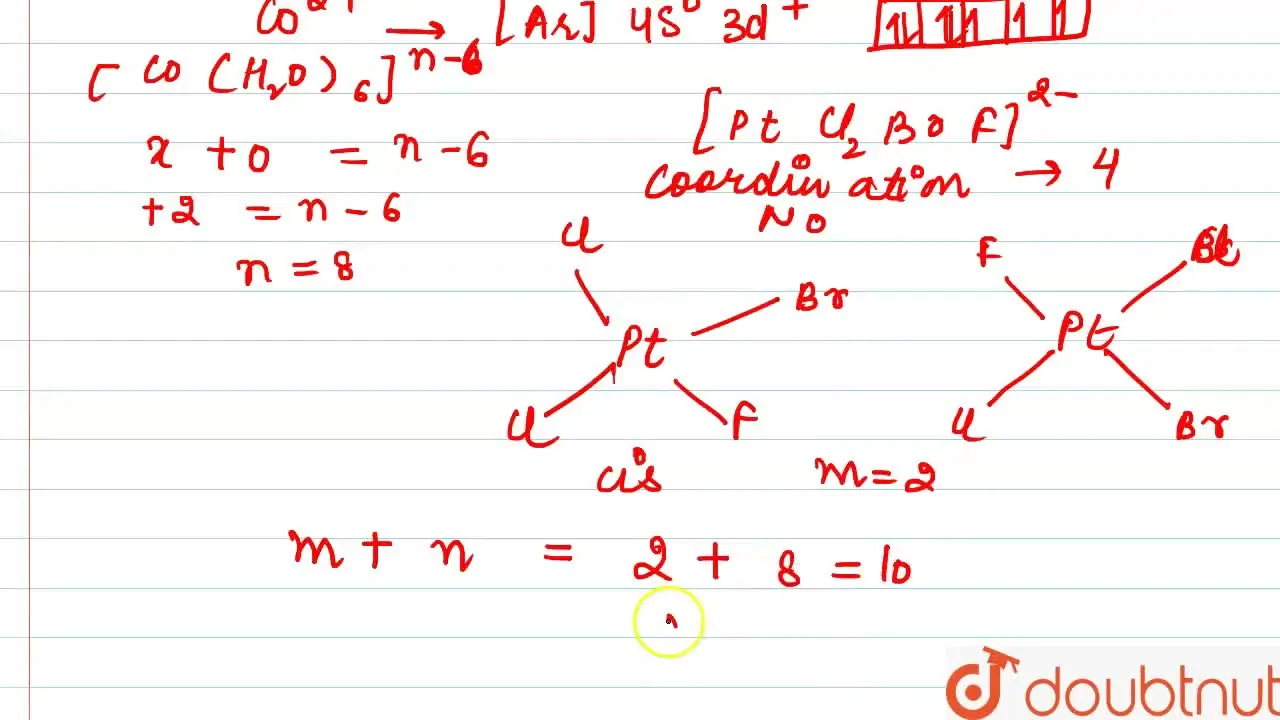
(i) [Co(H2O)6]n−6
(ii)[PtCl2BrF]2− m geometrical isomers
The spin only magnetic moment of complex (i) is 3.87 . The value of m+n is
8
9
10
11
(i) [Co(H2O)6]2+: number of unpaired e−=3,μ=√15B.M.
n−6=+2
n=+8
(ii) [PtCl2Brf]−2
dsp3 hybridization square planar, total three isomers
8+3=11
Related Playlists
Similar Questions
Spin only magnetic moment of [PtCl4]2− is
View SolutionThe spin only magnetic moment value of Cr(CO)6 is
View Solution[Co(H2O)6]3+ complex is
View SolutionCalculate the spin only magentic moment of M2+ ion (Z=27).
View SolutionSpin only magnetic moment of the compound Hg[Co(SCN)4] is √x B.M. The value of 'x' is
View SolutionHow many geometrical isomers are possible for complex [Mab(AB)2]n±?
View SolutionThe magnetic moment (spin only) of [NiCl4]2− is
View SolutionThe spin only magnetic moment of [MnBr_4]^(2-) is 5.9 B.M. Predict the geometry of the complex ion.
View SolutionConsider the follwing complexes ion P,Q and R
P=[FeF6]3−,Q=[V(H2O)6]2+ and R=[Fe(H2O)6]2+
The correct order of the complex ions, according to their spin only magnetic moment values (inBM) is .View SolutionConsider that a d6 metal ion (M2+) forms a complex with aqua ligands , and the spin only magnetic moment of the complex is 4.90 BM . The geometry and the crystal field stabilization energy of the complex is :
View Solution