In the following reaction, xA→yB
log10[−d[A]dt]=log10[d([B])dt]+0.3010 ‘A’ and ‘B’ respectively can be:
C2H2andC6H6
2C2H4andC4H8
N2O4andNO2
n - Butane and iso - butane
The correct Answer is:B
To solve the problem, we start with the given equation:
log10(−d(A)dt)=log10(d(B)dt)+0.3010
Step 1: Understand the logarithmic relationship
The equation can be interpreted using properties of logarithms. The term 0.3010 is equivalent to log10(2), since 100.3010≈2. Therefore, we can rewrite the equation as:
log10(−d(A)dt)=log10(d(B)dt)+log10(2)
Step 2: Use properties of logarithms
Using the property of logarithms that states log(a)+log(b)=log(ab), we can combine the right-hand side:
log10(−d(A)dt)=log10(2⋅d(B)dt)
Step 3: Remove the logarithm
By taking the antilogarithm of both sides, we can eliminate the logarithm:
−d(A)dt=2⋅d(B)dt
Step 4: Rearranging the equation
Rearranging this equation gives us:
d(A)dt=−2⋅d(B)dt
Step 5: Interpret the stoichiometry
This relationship indicates that for every 2 moles of B produced, 1 mole of A is consumed. This suggests a stoichiometric ratio of:
A→2B
Conclusion
Thus, the chemical reaction can be represented as:
2A→B
From the options given, we can conclude that the correct answer is that A and B are related by a stoichiometric coefficient of 2 for A and 1 for B.
The equation can be interpreted using properties of logarithms. The term 0.3010 is equivalent to log10(2), since 100.3010≈2. Therefore, we can rewrite the equation as:
Using the property of logarithms that states log(a)+log(b)=log(ab), we can combine the right-hand side:
By taking the antilogarithm of both sides, we can eliminate the logarithm:
Rearranging this equation gives us:
This relationship indicates that for every 2 moles of B produced, 1 mole of A is consumed. This suggests a stoichiometric ratio of:
Thus, the chemical reaction can be represented as:
Topper's Solved these Questions
- JEE MAIN REVISION TEST- 16Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST- 16Exercise:CHEMISTRY (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST 8 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST 8 (2020)Exercise:CHEMISTRY (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST- 24 Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST- 24 Exercise:CHEMISTRY (SECTION - 2)
Explore 5 Videos
Similar Questions
For the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionFor the reaction : aA→bB, it is given that
log[−dAdt]=log[dBdt]+0.6020. What is a:b is ?
View SolutionMechanism of the reaction is:
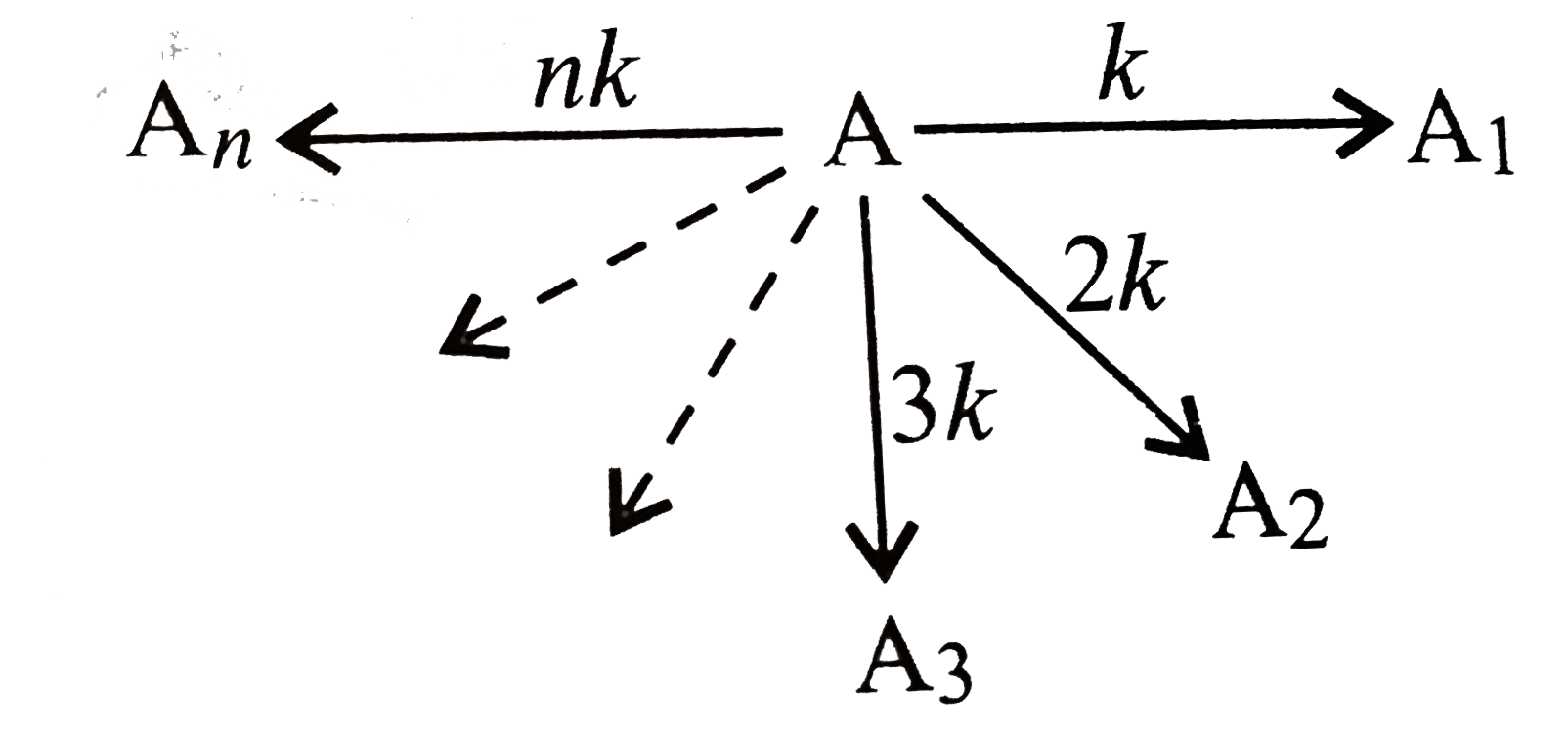
What is (a) −d[A]dt, (b) d[A1]dt
View SolutionDifferentiate the following w.r.t.x. log10x+logx10+logxx+log1010
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionMechanism of the reaction is:
What is −d[A]dt ?
View SolutionIf log105=a and log103=b,then
View SolutionFor the reaction 2A→B+3C, if −d[A]dt=k1[A]2,−d[B]dt=k2[A]2,−d[C]dt=k3[A]2 the correct reaction between k1,k2 and k3 is :
View SolutionExpress the following in exponential form:
a) log232=5
b) log√24=4
c) log100.01=−2
View SolutionDifferentiate the following functions with respect to x: (log)10x+(log)x10+(log)×+(log)1010
View Solution

