Decomposition of X exhibits a rate constant of 0.5μg/ year. How many years are required for the decomposition of 5μg of X into 2.5μg ?
The correct Answer is:5
To solve the problem of how many years are required for the decomposition of 5 micrograms of X into 2.5 micrograms, we follow these steps:
1. Identify the Reaction Order:
- We are given the rate constant k=0.5μg/year.
- The units of the rate constant suggest that this is a zero-order reaction because the unit of k is mass per time (i.e., μg/year).
2. Write the Zero-Order Reaction Equation:
- For a zero-order reaction, the relationship between the initial concentration A0, final concentration A, rate constant k, and time t is given by:
A=A0−kt
- Here, A0=5μg (initial amount), A=2.5μg (final amount), and k=0.5μg/year.
3. Substitute the Known Values into the Equation:
- Substitute the values into the equation:
2.5μg=5μg−(0.5μg/year)⋅t
4. Rearrange the Equation to Solve for Time t:
- Rearranging gives:
0.5μg/year⋅t=5μg−2.5μg
0.5μg/year⋅t=2.5μg
5. Solve for t:
- Divide both sides by 0.5μg/year:
t=2.5μg0.5μg/year=5years
Final Answer:
The time required for the decomposition of 5 micrograms of X into 2.5 micrograms is 5 years.
---
- We are given the rate constant k=0.5μg/year.
- The units of the rate constant suggest that this is a zero-order reaction because the unit of k is mass per time (i.e., μg/year).
- For a zero-order reaction, the relationship between the initial concentration A0, final concentration A, rate constant k, and time t is given by:
A=A0−kt
- Here, A0=5μg (initial amount), A=2.5μg (final amount), and k=0.5μg/year.
- Substitute the values into the equation:
2.5μg=5μg−(0.5μg/year)⋅t
- Rearranging gives:
0.5μg/year⋅t=5μg−2.5μg
0.5μg/year⋅t=2.5μg
- Divide both sides by 0.5μg/year:
t=2.5μg0.5μg/year=5years
The time required for the decomposition of 5 micrograms of X into 2.5 micrograms is 5 years.
Topper's Solved these Questions
Similar Questions
Knowledge Check
How many moles of oxygen gas can be produced during electricity decomposition of 180 g of water ?
A2.5 molesB5 molesC10 molesD7 molesA first order reaction has a rate constant of 5×10−3s−1. How long will 5.0g of this reaction take to reduce to 3.0g ?
A34.07 sB7.57 sC10.10 sD15 gConsider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given asAk=2.303tlogpipI−xBk=2.303tlog2pipI−xCk=2.303tlogpipI−ptDk=2.303tlogpipi−x
A block having 12 g of an element is placed in a room. This element is a radioactive element with a half-life of 15 years. After how many years will there be just 1.5 g of the element in the box ?
View SolutionSubstance A2B(g) can undergoes decomposition to form two set of products :
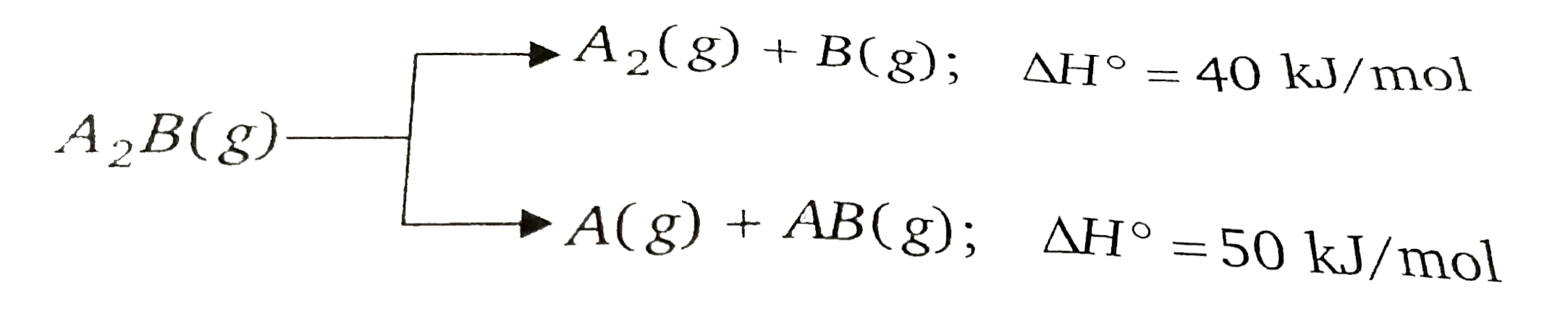
If the molar ratio of A2(g) to A(g) is 5:3 in a set of product gases, then the energy involved in the decomposition of 1 mole of A2B(g) is :
View SolutionSubstance A2B(g) can undergoes decomposition to form two set of products :
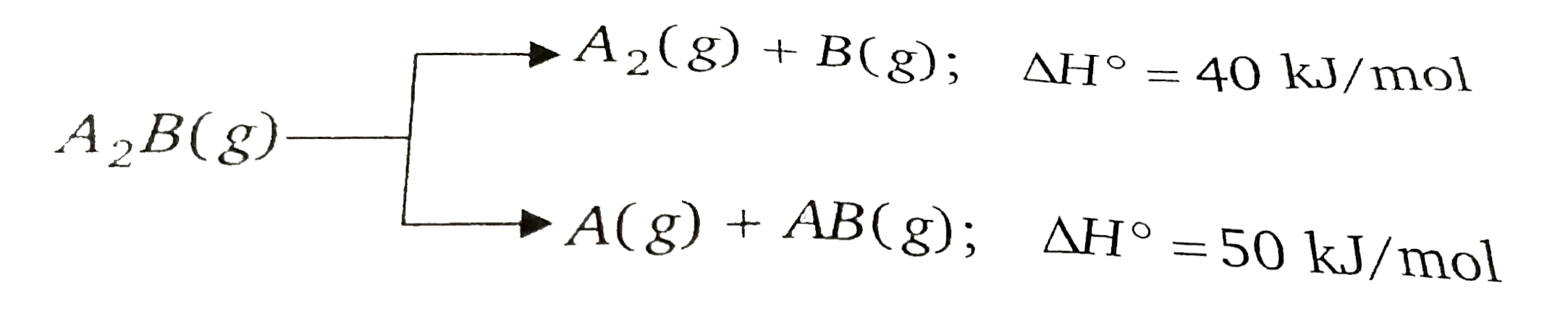
If the molar ratio of A2(g) to A(g) is 5:3 in a set of product gases, then the energy involved in the decomposition of 1 mole of A2B(g) is :
View SolutionConsider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given as
View SolutionConsider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given as
View Solution

