The Boolean expression ~(p⇒(~q)) is equivalent to:
(~p)⇒q
p∨q
p∧q
q⇒~q
The correct Answer is:C
To simplify the Boolean expression ~(p→(~q)), we can follow these steps:
Step 1: Rewrite the implication
The implication p→(~q) can be rewritten using the equivalence p→q≡~p∨q. Therefore, we can express p→(~q) as:
\(
p → (~q) \equiv ~p ∨ (~q)
\)
Step 2: Apply negation
Now, we need to apply the negation to the expression we obtained in Step 1:
\(
~(p → (~q)) \equiv ~(~p ∨ (~q))
\)
Step 3: Use De Morgan's Law
According to De Morgan's Law, the negation of a disjunction is equivalent to the conjunction of the negations:
\(
~(A ∨ B) \equiv ~A ∧ ~B
\)
Applying this to our expression:
\(
~(~p ∨ (~q)) \equiv ~~p ∧ ~~(~q)
\)
Step 4: Simplify double negation
The double negation can be simplified:
\(
~~p ∧ ~~(~q) \equiv p ∧ q
\)
Thus, the simplified expression is:
\(
p ∧ q
\)
Final Answer
The Boolean expression ~(p→(~q)) is equivalent to:
\(
p ∧ q
\)
The implication p→(~q) can be rewritten using the equivalence p→q≡~p∨q. Therefore, we can express p→(~q) as:
\(
p → (~q) \equiv ~p ∨ (~q)
\)
Now, we need to apply the negation to the expression we obtained in Step 1:
\(
~(p → (~q)) \equiv ~(~p ∨ (~q))
\)
According to De Morgan's Law, the negation of a disjunction is equivalent to the conjunction of the negations:
\(
~(A ∨ B) \equiv ~A ∧ ~B
\)
Applying this to our expression:
\(
~(~p ∨ (~q)) \equiv ~~p ∧ ~~(~q)
\)
The double negation can be simplified:
\(
~~p ∧ ~~(~q) \equiv p ∧ q
\)
\(
p ∧ q
\)
The Boolean expression ~(p→(~q)) is equivalent to:
\(
p ∧ q
\)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The Boolean expression for the given circuit is
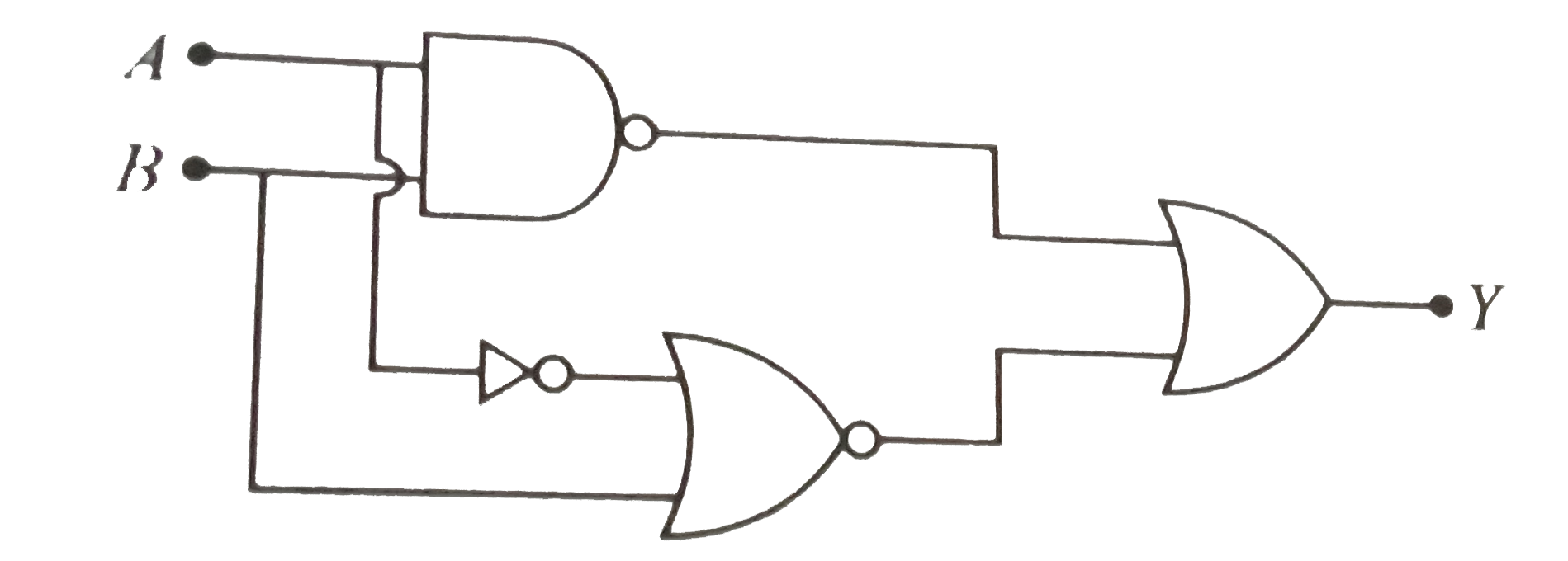 A¯¯¯¯¯¯¯¯A.BBA+BC¯¯¯A+BDA+¯¯¯B
A¯¯¯¯¯¯¯¯A.BBA+BC¯¯¯A+BDA+¯¯¯B
The Boolean Expression (p∧~q)∨q∨(~p∧q) is equivalent to :
View Solution~(p∨q)∨(~p∧q) is equivalent to
View SolutionThe statement (~(p⇔q))∧p is equivalent to
View SolutionThe proposition ~p∨(p∧~q) is equivalent to
View SolutionIf the Boolean expression (p⊕q)∧(~pΘq) is equivalent to p∧q, where ⊕,Θ∈{∨,∧}, then the ordered pair (⊕,Θ) is
View SolutionUsing truth table, prove that ~(p⇔~q) is equivalent to p⇔q.
View Solutionp→q is logically equivalent to
View Solution

