A person throws two pair dice. He wins Rs. 15 for throwing a doublet (same numbers on the two dice), wins Rs. 12 when the throw results in the sum of 9, and loses Rs.6 for any other outcome on the throw. Then the expected gain/loss (in Rs.) of the person is:
A. 12 gain
B.14 loss
C. 2 gain
D. 12 loss
The correct Answer is:D
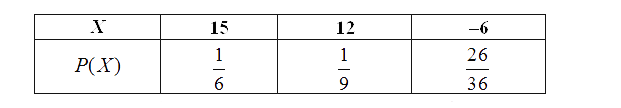
Expectationi =156+129−6×2636=15+8−266=−12
Topper's Solved these Questions
Similar Questions
In a game, a man wins Rs 100 if he gets 5 or 6 on a throw of a fair die and loses Rs 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is:
(a) 4003 gain
(b) 4009 loss
(c) 0
(d) 4003 loss
View SolutionIn a game, a man wins Rs 100 if he gets 5 or 6 on a throw of a fair die and loses Rs 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is: (a) 4003 gain (b) 4009 loss (c) 0 (d) 4003 loss
View SolutionIn a single throw of two dice , what is the probability of
a doublet of even number
View SolutionIn a single throw of two dice, determine the probability of not getting the same number on both the dice.
View SolutionIn one throw of two dice together, find the probability of getting:
(i) a sum of 5
(ii) same number on two dice
View SolutionThe sum of numbers on two throws of a dice is 8. Find the probability of getting 3 in at least one throw.
View SolutionFind the probability of getting the same number of two dice in a single throw of two dice.
View SolutionGiven that the two numbers appearing on throwing two dice are different. Find the probability of the event the sum of numbers on the dice is 4.
View SolutionA person throws two dice, one the common cube and the other a regular tetrahedron, the number on the lowest face being taken in the case of the tetrahedron, then find the probability that the sum of the numberd appearing on the dice is 6.
View SolutionIt is know that the numbers getting in one throw of two dice are different. Find the probability of getting a sum of 6.
View Solution

