ABC is a triangular park with AB=AC=100 m .A clock tower is situated at the midpoint of BC. The angle of elevation α and β of the top of the tower at A and B, respectively ,are such that cot α =3.2 cosec β = 2.6 Find the height of the tower .
1003√3
25
20
10√5
The correct Answer is:C
Let h(m) be the height of the tower
Say BM=d
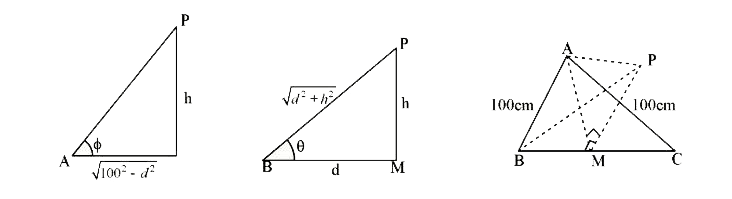
θ=cosec−12√2
2√2=√d2−d2h
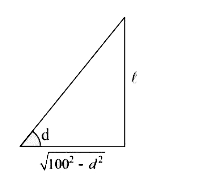
cotϕ=√(100)2−d2h
3√2=√(100)2−d2h
18h2=1002−d2...........(2)
Put the values of d2 from (1) and (2)
18h2=1002−7h2⇒25h2=100×100
h=20 m
Topper's Solved these Questions
- JEE MAIN REVISION TEST -14 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -14 EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 7|JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Mathematics (Section - 2) Numercial type questions
5 Videos
- JEE MAIN REVISION TEST -17 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -17 (2020)EXERCISE - MATHEMATICS
25 Videos
Similar Questions
ABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are cot−1(3.2) and cosec−1(2.6) respectively.The height of the tower is:
View SolutionPQR is a triangular park with PQ=PR=200m . A T.V tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P , Q and R respectively 45∘ , 30∘ and 30∘ then the height of the tower in m is
View Solution
Knowledge Check
The angle of elevation of the top of a tower. from a point on the ground and at a distance of 160 m from its foot, is find to be 60∘ . Find the height of the tower .
A277.12 mB377.12 mC477.12 mDNone
PQR is a triangular park with PQ=PR=200m . A T.V tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P , Q and R respectively 45∘ , 30∘ and 30∘ then the height of the tower in m is
View SolutionPQR is a triangular park with PQ=PR=200m. A.T.V. tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P, Q and R are respectively 45o–, 30o– and 30o– then the height of the tower (in m ) is
View SolutionThe persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30∘and38∘ respectively. Find the distance between them, if the height of the tower is 50 m
View SolutionThe angles of the depression of the top and bottom of the tower is seen from the top of a 60√3 cliff are 45α and 60α respectively. Find the height of the tower.
View SolutionThe angles of the depression of the top and bottom of the tower is seen from the top of a 60√3 cliff are 45α and 60α respectively. Find the height of the tower.
View SolutionThe angles of the depression of the top and bottom of the tower is seen from the top of a 60√3 cliff are 45α and 60α respectively. Find the height of the tower.
View Solution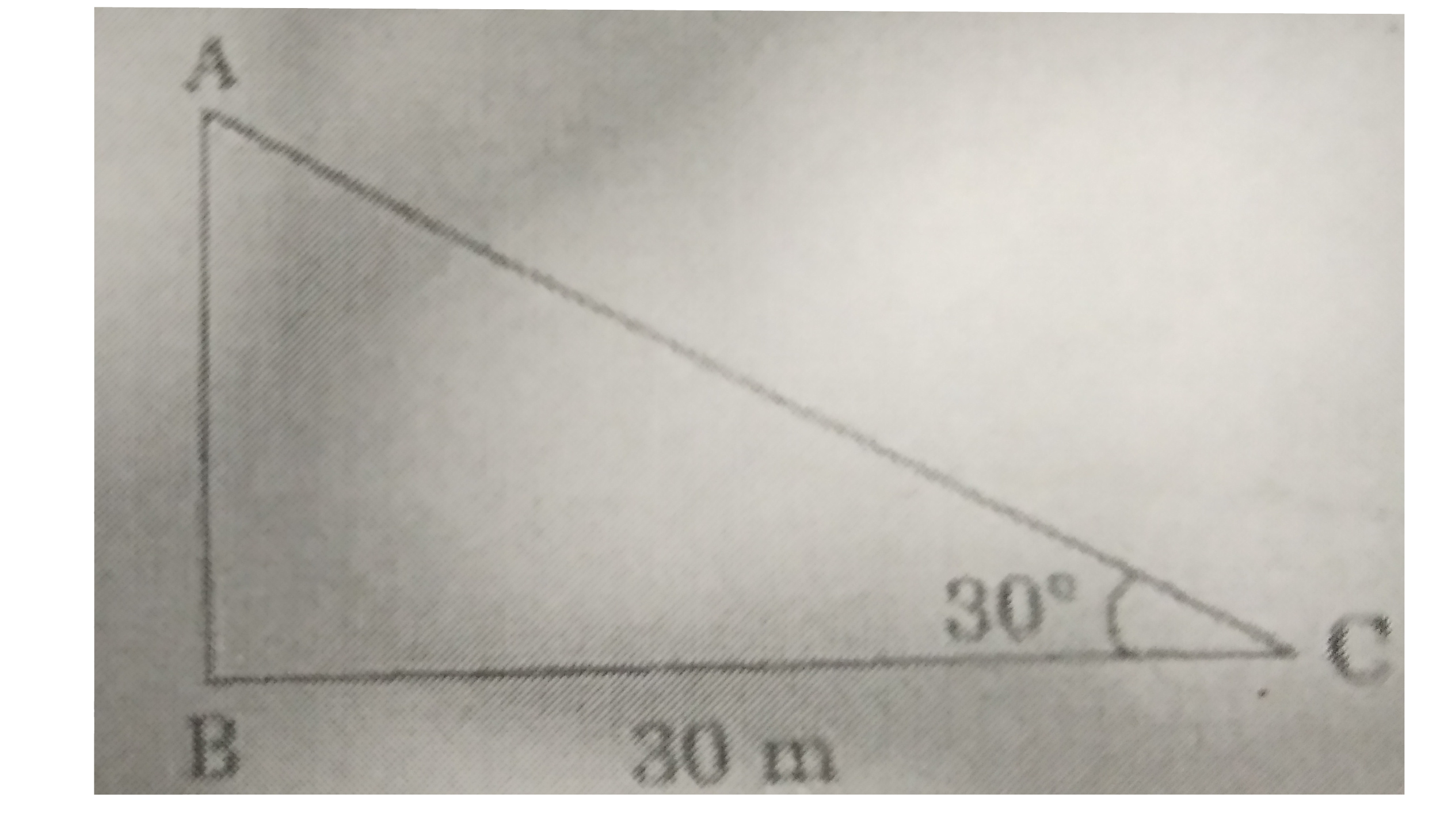
If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is 30∘. Find th height of the tower.
View Solution
