ABC is a triangular park with AB = AC = 100 m. A block tower is situated at the midpoint of BC.The angles of elevation of the top of the tower at A and B are ${cot}^{- 1} (3.2)$ and $cos e c^{- 1} (2.6)$ respectively.The height of the tower is:

Video Solution

Text Solution

Verified by Experts

In the figure DP is a clock tower of height 'h' standing at D, the midpoint of BC.

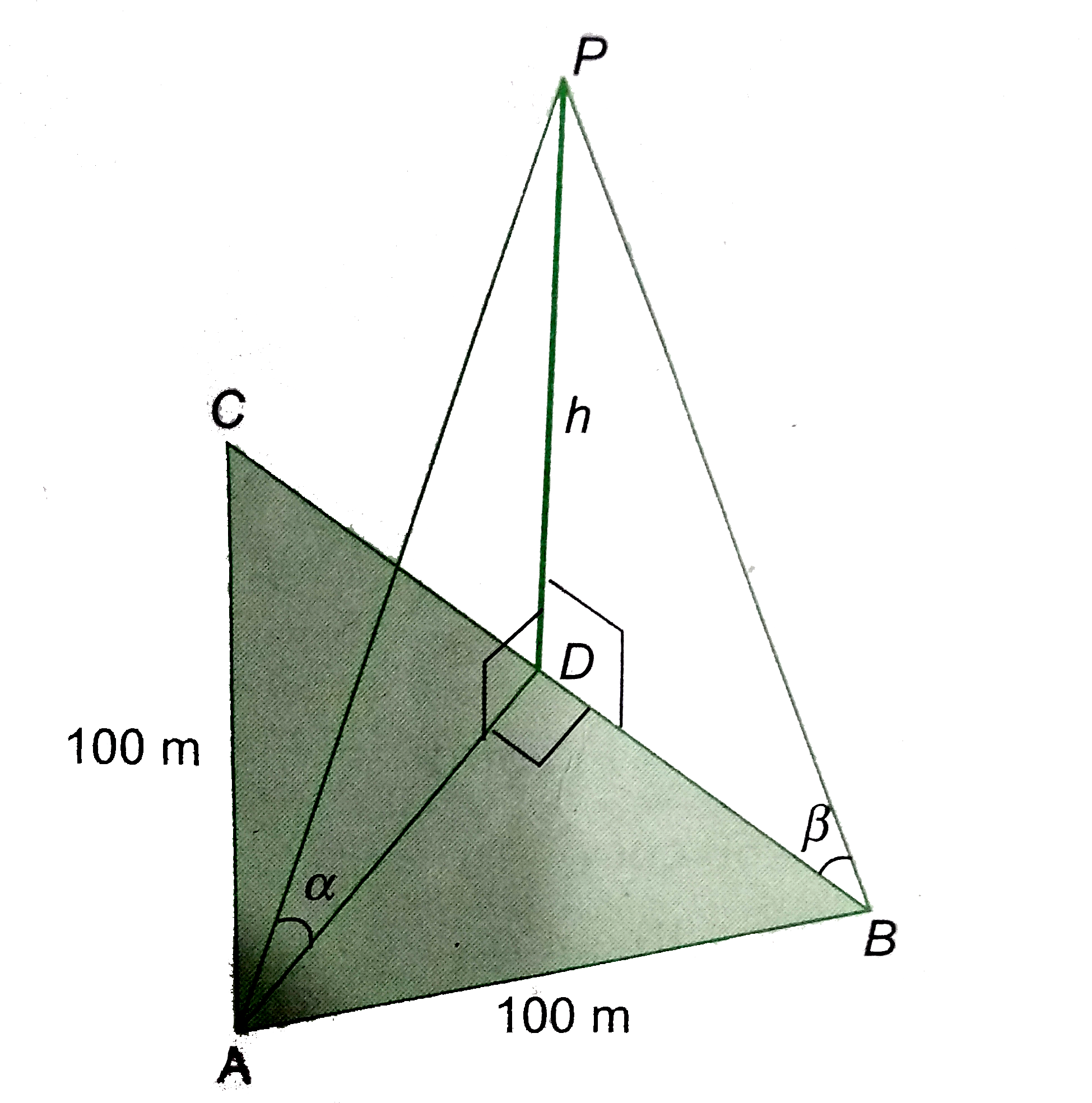
since AB=AC ,AD is perpendicular to BC. In triangle ADP.
$tan α = \frac{h}{A D}$
$\Rightarrow A D cot α$
In triangle PDB ,
$tan β = \frac{h}{B D}$
$\Rightarrow B D = h cot β$
Now ,in right triangle ADB,
$A B^{2} + A D^{2} + B D^{2}$
$\Rightarrow 100^{2} = h^{2} {cot}^{2} α + h^{2} {cot}^{2} + β$
$\Rightarrow 100^{2} = h^{2} [{cot}^{2} α + (cos e c^{2} β - 1)]$
$\Rightarrow 100^{2} = h^{2} [{(3.2)}^{2} + {(2.6)}^{2} - 1)]$
$\Rightarrow 100^{2} = 16 h^{2}$
$\Rightarrow h^{2} = 625$
$\Rightarrow h = 25 m$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-HIGHT AND DISTANCE -Archives

Home
Ask Doubt
Profile