A metal coinn of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass as shown in the figure. The system is initially at rest. The constant torque, hat will make the system rotate about AB at 25 rotations per second in 5s. Is close to

1.6×10−5Nm
7.9×10−6Nm
2.0×10−5Nm
4.0×10−6Nm
The correct Answer is:C
α=ωf−ωiΔt=25×2π5=10πrads2
τ=Iα=(MR24+MR2)α=54MR2=1.96×10−5□2.0×10−5Nm
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 13BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 13EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 12 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 12 EXERCISE - PHYSICS
25 Videos
- JEE MAIN REVISION TEST - 18BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 18EXERCISE - PHYSICS - SECTION 2
5 Videos
Similar Questions
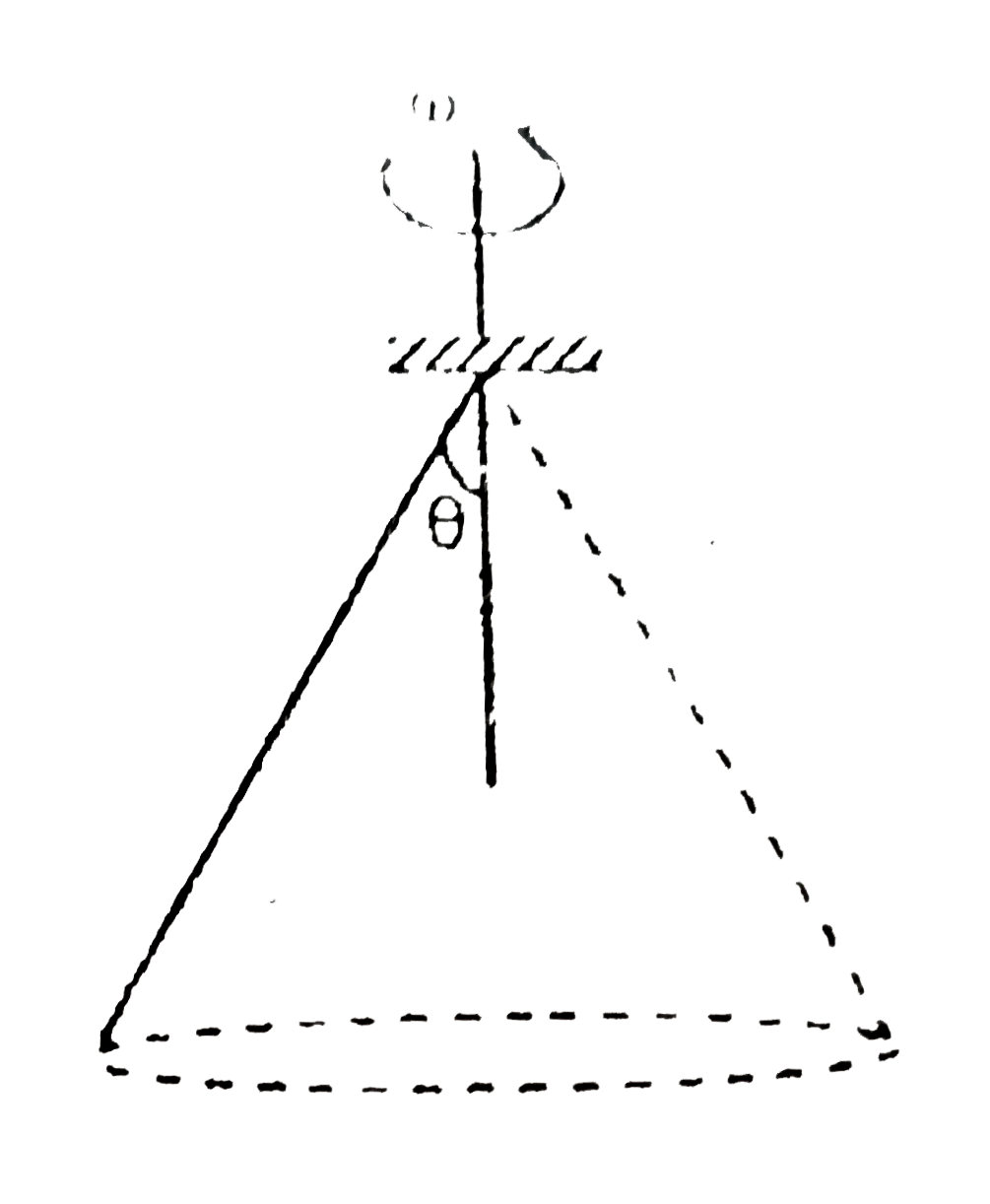
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
View SolutionTwo discs A and B each of mass 2kg and radius 0.5m are rigidly fixed to the end of a thin shaft S, which is supported in horizontal position with the help of two smooth bearings at points P1 and P2. Two blocks of masses 2kg and 1kg are connected to the light cords wrapped around the discs as shown in the figure. There is no slipping between the cord and the discs. If the system is released from rest from the position shown, the mark released from rest from the position shown,

View Solution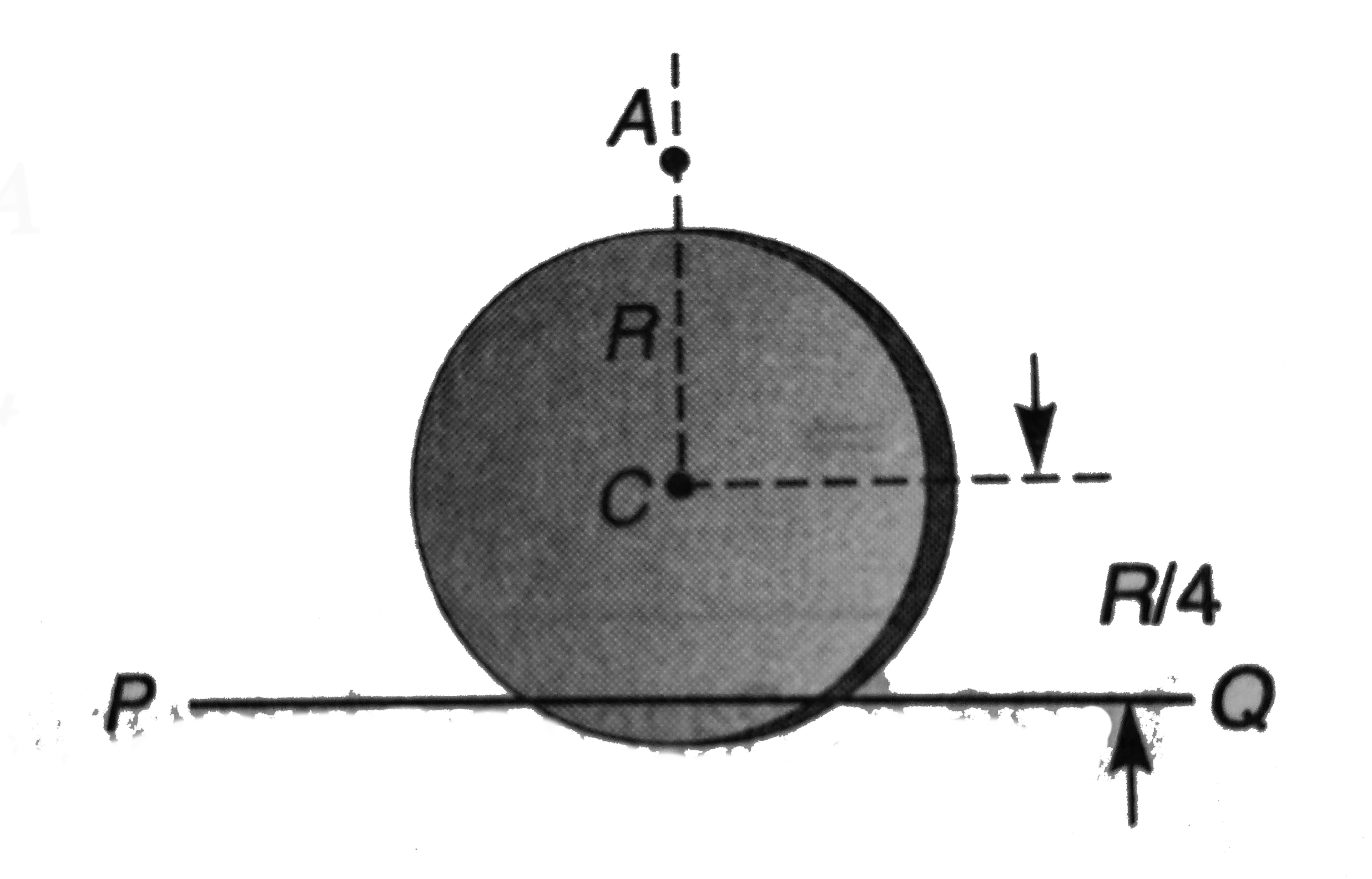
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
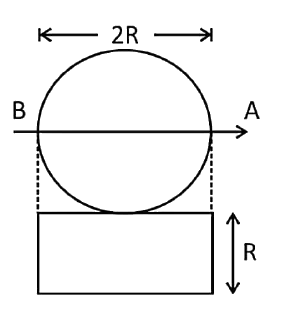
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
View SolutionA whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of 2πrad/s the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
View SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass M of 2kg attached to it at a distance of 1m from the wall. A mass m of 0.5kg is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? (g=10ms−2)
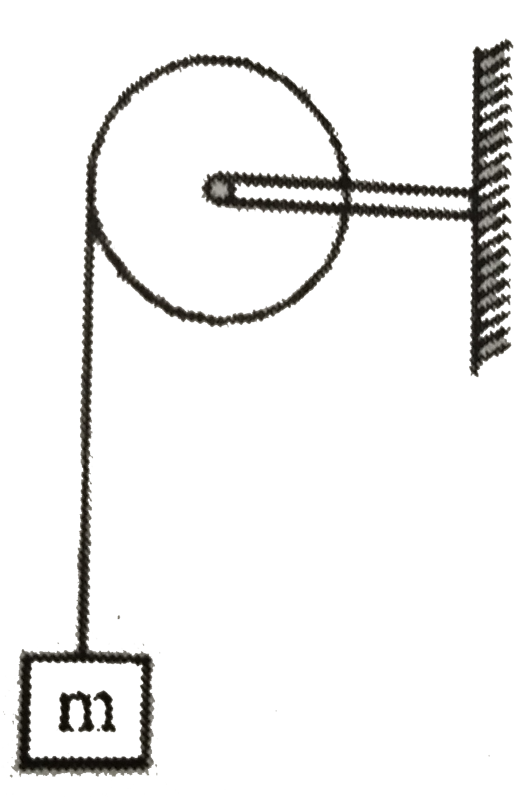
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
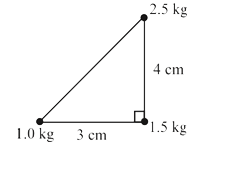
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

View SolutionThree particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
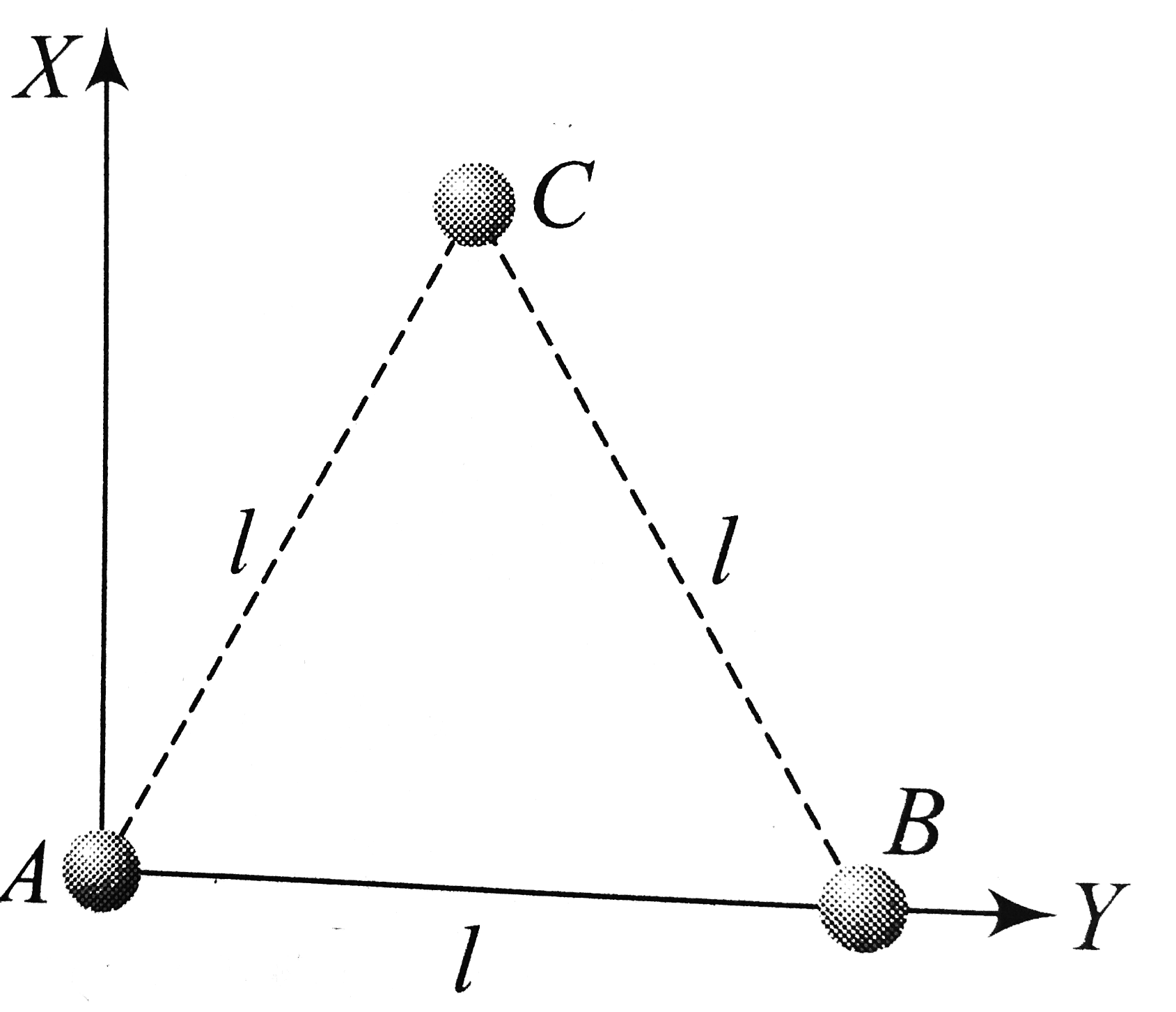 .
.
View Solution
