A wedge of mass M = 4m lies on a frictionless plane. A particle of mass m approaches the wedge with speed v. There is no friction between the particle and the plane or between the particle and the wedge. The maximum height climbed by the particle on the wedge is given by:
2v25g
v2g
2v27g
v22g
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the system
We have a wedge of mass M=4m on a frictionless plane and a particle of mass m approaching the wedge with speed v. The goal is to find the maximum height h that the particle climbs on the wedge.
Step 2: Apply conservation of momentum
Before the collision, the total momentum of the system is given by the momentum of the particle:
Pinitial=mv
After the collision, the wedge and the particle move together with a common velocity v0. The total mass after the collision is m+4m=5m. Therefore, the final momentum is:
Pfinal=(m+4m)v0=5mv0
By conservation of momentum:
mv=5mv0
From this, we can solve for v0:
v0=v5
Step 3: Apply conservation of energy
Initially, the particle has kinetic energy and no potential energy:
KEinitial=12mv2
At the maximum height h, the particle has potential energy and kinetic energy. The potential energy is given by:
PEfinal=mgh
The kinetic energy of the wedge and the particle after the collision is:
KEfinal=12(m+4m)v20=12(5m)(v5)2=12(5m)v225=mv210
By conservation of energy:
KEinitial=PEfinal+KEfinal
Substituting the values we found:
12mv2=mgh+mv210
Step 4: Solve for height h
Rearranging the equation gives:
12mv2−mv210=mgh
Factoring out m:
m(12v2−110v2)=mgh
Simplifying the left side:
510v2−110v2=410v2=25v2
Thus, we have:
25v2=gh
Solving for h:
h=2v25g
Final Answer
The maximum height climbed by the particle on the wedge is:
h=2v25g
We have a wedge of mass M=4m on a frictionless plane and a particle of mass m approaching the wedge with speed v. The goal is to find the maximum height h that the particle climbs on the wedge.
Before the collision, the total momentum of the system is given by the momentum of the particle:
Pinitial=mv
After the collision, the wedge and the particle move together with a common velocity v0. The total mass after the collision is m+4m=5m. Therefore, the final momentum is:
Pfinal=(m+4m)v0=5mv0
By conservation of momentum:
mv=5mv0
From this, we can solve for v0:
v0=v5
Initially, the particle has kinetic energy and no potential energy:
KEinitial=12mv2
At the maximum height h, the particle has potential energy and kinetic energy. The potential energy is given by:
PEfinal=mgh
The kinetic energy of the wedge and the particle after the collision is:
KEfinal=12(m+4m)v20=12(5m)(v5)2=12(5m)v225=mv210
By conservation of energy:
KEinitial=PEfinal+KEfinal
Substituting the values we found:
12mv2=mgh+mv210
Rearranging the equation gives:
12mv2−mv210=mgh
Factoring out m:
m(12v2−110v2)=mgh
Simplifying the left side:
510v2−110v2=410v2=25v2
Thus, we have:
25v2=gh
Solving for h:
h=2v25g
The maximum height climbed by the particle on the wedge is:
h=2v25g
Topper's Solved these Questions
- JEE MAIN REVISION TEST 11 (2020) BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 11 (2020) EXERCISE - PHYSICS (SECTION - 2)
5 Videos
- JEE MAIN REVISION TEST -17 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -17 (2020)EXERCISE - PHYSICS
25 Videos
- JEE MAIN REVISION TEST 5 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 5 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
Similar Questions
a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
View SolutionA wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e.
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
View Solution

In the situation shown in figure a wedge of mass m is placed on a rough surface, on which a block of equal mass is placed on the inclined plane of wedge.Friction coefficient between plane and the block and the ground and the wedge (μ). An external force F is applied horizontally on the wedge. Given the m does not slide on incline due to its weight. The value of F at which wedge will start slipping is:
View SolutionFind the displacement of the wedge when m comes out of the wedge. There is no friction anywhere.

View SolutionA wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
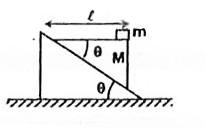
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.
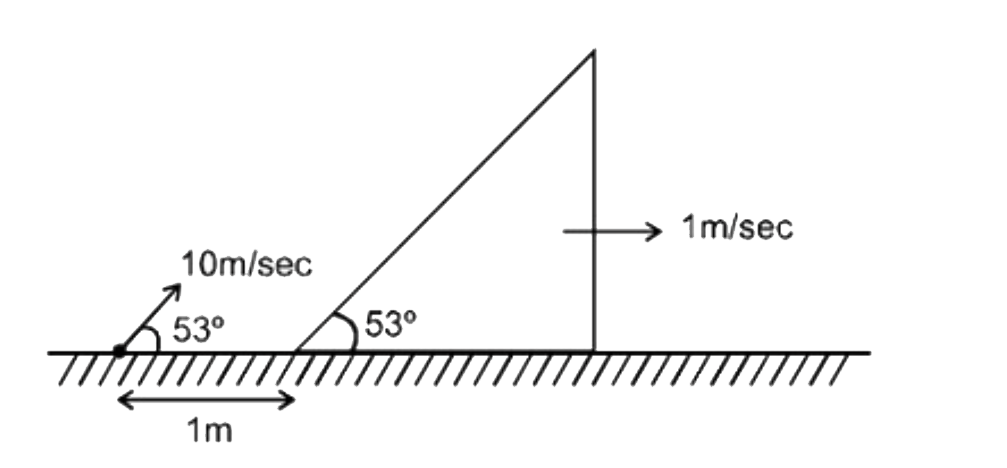
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]
View SolutionA wedge of mass m2 is kept on a spring balance. A small block of mass m1 can move along the frictionless incline of the wedge. What is the reading of the balance while the block slides? Ignore the recoil of the wedge.

View SolutionTwo wedges, each of mass m, are placed next to each other on a flat horizontal floor. A cube of mass M is balanced on the wedges as shown in figure. Assume no friction between the cube and the wedges, but a coefficent of static friction μ<1 between the wedges and the floor. What is the largest M that can be balanced as shown without motion of the wedges ?

View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View Solution
