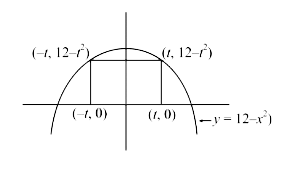
Find the are of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
20√2
18√3
32
36
The correct Answer is:C
Area =A=2t(12−t2)
dAdt=24−6t2.
For maximum value of A,dAdt=0
24−6t2=0,t=±2
A=2t(12−t2)=32 .
 .
.
Topper's Solved these Questions
- JEE MAIN REVISION TEST 8 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 8 (2020)EXERCISE - MATHEMATICS ( SECTION 2 )
5 Videos
- JEE MAIN REVISION TEST 5 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 5 (2020)EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST- 16BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 16EXERCISE - MATHEMATICS (SECTION 2)
5 Videos
Similar Questions
Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionFind the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:

View SolutionFind the area bounded by the curve y=e−x the X-axis and the Y-axis.
View SolutionFind the area of the region enclosed by the curves
y=x2−4x+3 and the x-axis
View SolutionFind the area between x-axis and the curve y=(x−1)2−25.
View SolutionFind the area of that region bounded by the curve y=cosx, X-axis, x=0 and x=π.
View SolutionFind the area of the region bounded by the curves x=4y−y2 and the Y-axis.
View SolutionLet a parabola be y=12−x2. Find the maximum area of rectangle whose base lie on x-axis and two points lie on parabola. (A) 8 (B) 4 (C) 32 (D) 34
View Solution
