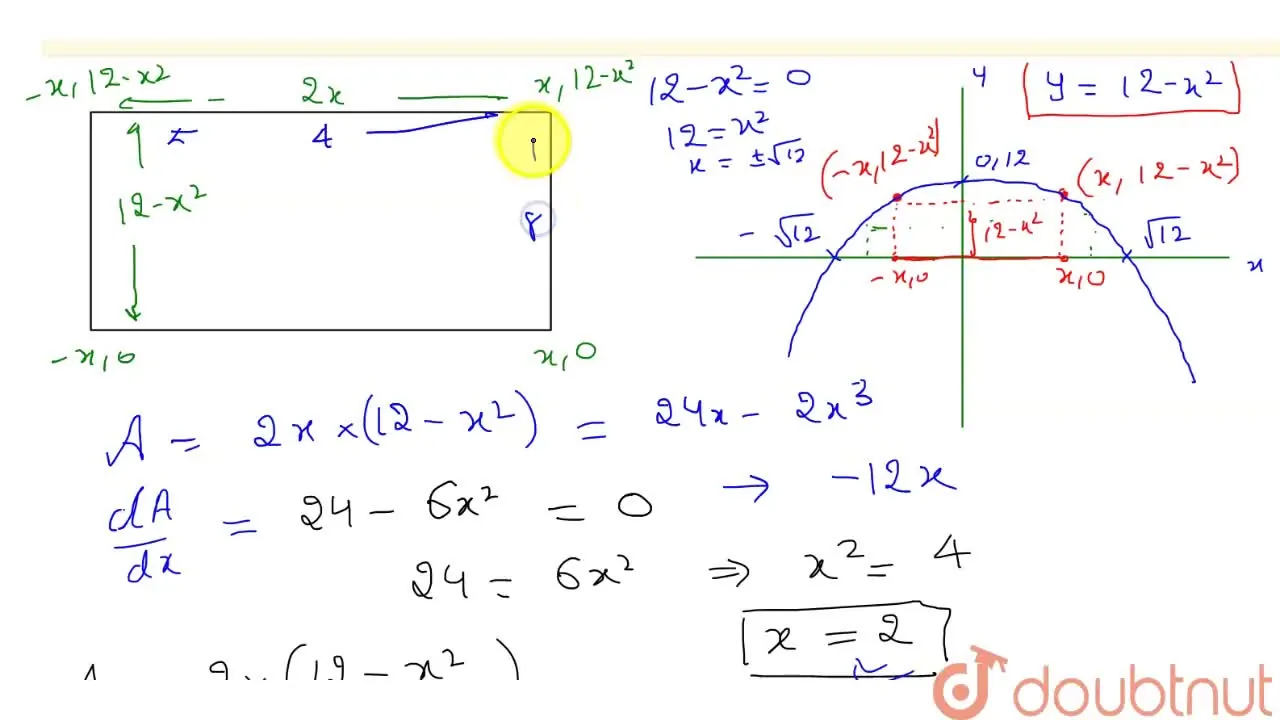
Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
The correct Answer is:32 sq. units
Step by step video & image solution for Find the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12-x^2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1F9videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise Part II -1A9videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise -1D11videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)5videos
COMBINATORICS
Similar Questions
The largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionFind the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
View SolutionFour particles, each with mass m are arranged symmetrically about the origin on the x axis. A fifth particle, with mass M, is on the y axis. The direction of the gravitational force on M is:
 View Solution
View SolutionFind the area bounded by the curve y=e−x the X-axis and the Y-axis.
View SolutionFind the area of the region enclosed by the curves
y=x2−4x+3 and the x-axisView SolutionFind the area of that region bounded by the curve y=cosx, X-axis, x=0 and x=π.
View SolutionFind the area between the curve y=x and y=x2
View SolutionFind the area of the region bounded by the curves x=4y−y2 and the Y-axis.
View SolutionFind the area between x-axis and the curve y=(x−1)2−25.
View SolutionFind the area of the region bounded by the curve y=x2−2x, the x-axis and the lines x=1andx=−1
View Solution