Question

Two solids dissociates as follows
.
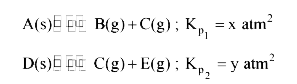The total pressure when both the solids dissociate simultaneously is :

1. $2\left(\sqrt{x+y}\right)$ atm

2. $(x+y)$ atm

3. $\sqrt{x+y}$ atm

4. $x^2+y^2$.

Options

A. `2 (sqrt(x+y))` atm
B. `(x+y)` atm
C. `sqrt(x+y)` atm
D. `x^2+y^2`.

Answer

A

Explanation

.
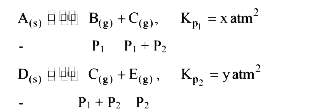`Kp_(1)=P_(1)(P_1+P_2)=x`
`Kp_(2)=P_(2)(P_1+P_2)=y`
`therefore Kp_(1)+Kp_(2)=(P_(1)+P_(2))^2=x+y rArr P_(1)+P_(2)sqrt(x+y) rArr 2(P_1+P_2)=2sqrt(x+y)`
`therefore P_("total") =P_(B)+P_(C)+P_(E)=2(P_1+P_2)=2sqrt(x+y)`.