There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its intantanradius R(t) is :
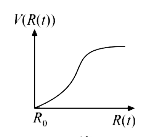
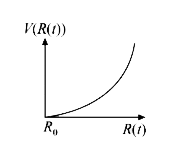
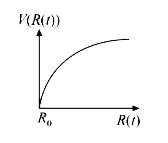

The correct Answer is:C
To solve the problem, we need to analyze the expansion of a uniform spherically symmetric surface charge density due to mutual repulsion. We'll derive the relationship between the speed V(r(t)) of the distribution and its instantaneous radius R(t).
1. Understanding the System:
- We have a uniform spherically symmetric surface charge density at an initial radius R0.
- The charge distribution is initially at rest and starts expanding due to mutual repulsion among the charges.
2. Applying Work-Energy Theorem:
- Since there are no external forces acting on the system, the work done by external forces is zero.
- According to the work-energy theorem, the work done by all forces is equal to the change in kinetic energy:
Wtotal=ΔKE
3. Identifying Forces:
- The only forces doing work are the electric forces due to the surface charge. The work done by the electric field can be expressed as:
W=Ufinal−Uinitial
- Here, U is the electric potential energy.
4. Calculating Electric Potential Energy:
- The potential energy U for a uniformly charged sphere can be expressed as:
U=KQ22R
- Where K is Coulomb's constant, Q is the total charge, and R is the radius.
5. Setting Up the Energy Equation:
- Initially, at radius R0:
Uinitial=KQ22R0
- At an instantaneous radius R:
Ufinal=KQ22R
- The change in kinetic energy is given by:
KE=12MV2
6. Equating Energies:
- Setting the work done equal to the change in kinetic energy:
KQ22R−KQ22R0=12MV2
- Rearranging gives:
KQ22R−KQ22R0=12MV2
7. Solving for Speed V:
- Rearranging the equation, we find:
MV2=KQ2(1R−1R0)
- Thus, the speed V can be expressed as:
V=√KQ2M(1R0−1R)
8. Differentiating with Respect to Radius:
- To understand how V changes with R, we differentiate:
dVdR=KQ2M⋅12V⋅(−1R2)
- This shows that dVdR is negative, indicating that as R increases, V decreases.
9. Conclusion:
- The speed V as a function of the instantaneous radius R decreases with increasing R. This means that the graph of V versus R will have a negative slope.
Final Answer:
The correct figure that represents the speed V(r(t)) of the distribution as a function of its instantaneous radius R(t) is option third.
- We have a uniform spherically symmetric surface charge density at an initial radius R0.
- The charge distribution is initially at rest and starts expanding due to mutual repulsion among the charges.
- Since there are no external forces acting on the system, the work done by external forces is zero.
- According to the work-energy theorem, the work done by all forces is equal to the change in kinetic energy:
Wtotal=ΔKE
- The only forces doing work are the electric forces due to the surface charge. The work done by the electric field can be expressed as:
W=Ufinal−Uinitial
- Here, U is the electric potential energy.
- The potential energy U for a uniformly charged sphere can be expressed as:
U=KQ22R
- Where K is Coulomb's constant, Q is the total charge, and R is the radius.
- Initially, at radius R0:
Uinitial=KQ22R0
- At an instantaneous radius R:
Ufinal=KQ22R
- The change in kinetic energy is given by:
KE=12MV2
- Setting the work done equal to the change in kinetic energy:
KQ22R−KQ22R0=12MV2
- Rearranging gives:
KQ22R−KQ22R0=12MV2
- Rearranging the equation, we find:
MV2=KQ2(1R−1R0)
- Thus, the speed V can be expressed as:
V=√KQ2M(1R0−1R)
- To understand how V changes with R, we differentiate:
dVdR=KQ2M⋅12V⋅(−1R2)
- This shows that dVdR is negative, indicating that as R increases, V decreases.
- The speed V as a function of the instantaneous radius R decreases with increasing R. This means that the graph of V versus R will have a negative slope.
The correct figure that represents the speed V(r(t)) of the distribution as a function of its instantaneous radius R(t) is option third.
Topper's Solved these Questions
- JEE MAIN REVISION TEST 8 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST 8 (2020)Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST 5 (2020)Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST 5 (2020)Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST- 16Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST- 16Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
Similar Questions
There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its instant radius R(t) is :
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionFor spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View SolutionThe maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
View SolutionThe energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
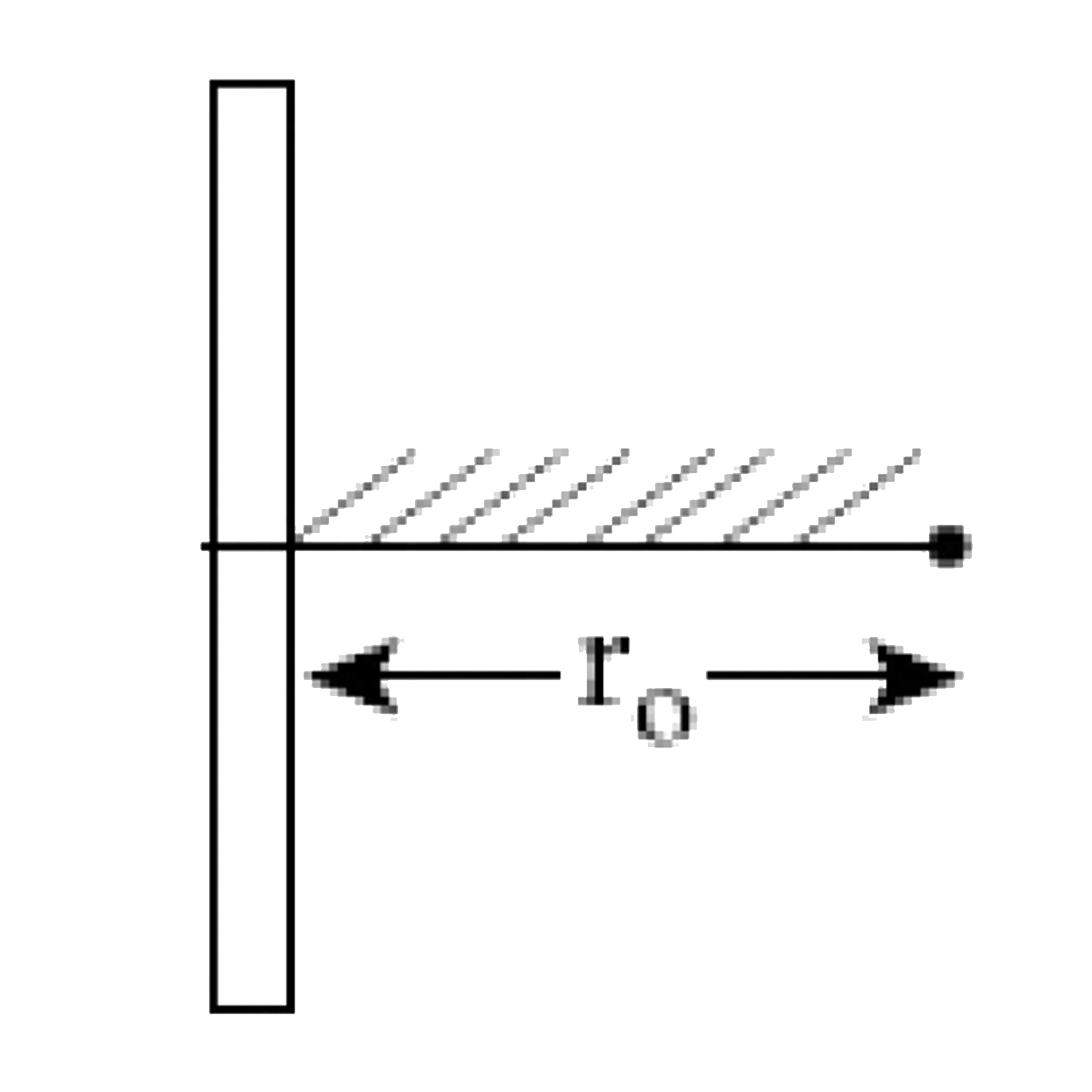
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionConsider a uniform spherical charge distribution of radius R1 centred at the origin O. In this distribution a spherical cavity of radius R2, centred at P with distance OP=a=R1−R2 (fig) is made.If the electric field inside the cavity at position →r, then the correct statement is
View Solution
