State True or False: If bxy<0 and byx<0 then ‘r’ is >0
The correct Answer is:False
To determine whether the statement "If bxy<0 and byx<0 then r>0" is true or false, we can analyze the relationship between the regression coefficients and the correlation coefficient.
1. Understanding the Regression Coefficients:
- The regression coefficients bxy and byx represent the relationship between two variables x and y.
- bxy indicates how y changes with respect to x, and byx indicates how x changes with respect to y.
2. Given Conditions:
- We are given that bxy<0 and byx<0. This means both regression coefficients are negative.
3. Relationship Between Regression Coefficients and Correlation Coefficient:
- There is a known relationship between the regression coefficients and the correlation coefficient r:
r2=bxy⋅byx
- This implies that the square of the correlation coefficient is equal to the product of the two regression coefficients.
4. Analyzing the Signs:
- Since both bxy<0 and byx<0, their product bxy⋅byx will be positive (as the product of two negative numbers is positive).
- Therefore, r2>0, which implies that r can be either positive or negative.
5. Determining the Sign of r:
- However, since both regression coefficients are negative, the correlation coefficient r will also be negative.
- This is because the correlation coefficient reflects the direction of the relationship: both variables decrease together, leading to a negative correlation.
6. Conclusion:
- Since we have established that r<0 given the conditions bxy<0 and byx<0, the statement "If bxy<0 and byx<0 then r>0" is FALSE.
Final Answer:
False
- The regression coefficients bxy and byx represent the relationship between two variables x and y.
- bxy indicates how y changes with respect to x, and byx indicates how x changes with respect to y.
- We are given that bxy<0 and byx<0. This means both regression coefficients are negative.
- There is a known relationship between the regression coefficients and the correlation coefficient r:
r2=bxy⋅byx
- This implies that the square of the correlation coefficient is equal to the product of the two regression coefficients.
- Since both bxy<0 and byx<0, their product bxy⋅byx will be positive (as the product of two negative numbers is positive).
- Therefore, r2>0, which implies that r can be either positive or negative.
- However, since both regression coefficients are negative, the correlation coefficient r will also be negative.
- This is because the correlation coefficient reflects the direction of the relationship: both variables decrease together, leading to a negative correlation.
- Since we have established that r<0 given the conditions bxy<0 and byx<0, the statement "If bxy<0 and byx<0 then r>0" is FALSE.
False
Topper's Solved these Questions
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 3. LINEAR REGRESSION (III. Fill in the following blanks:)
Explore 11 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 3. LINEAR REGRESSION (IV.Answer the following:)
Explore 15 Videos
- QUESTION BANK 2021Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:QUESTION BANK 2021Exercise:Part II 3. LINEAR REGRESSION (I Select and write the most appropriate answer from given alternatives of the following sub questions:)
Explore 17 Videos
- PROBABILITY DISTRIBUTIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY DISTRIBUTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:THREE DIMENSIONAL GEOMETRY Exercise:MULTIPLE CHOICE QUESTIONS
Explore 8 Videos
Similar Questions
State True or False: If byx=1.5 and bxy=13 then r=12. The given data is consistent.
View SolutionState which of the following statements is true of false.
(i) If x<yandb<0, then xb<yb.
(ii) If xy>0, then x>0andy<0
(iii) If xy>0, then x<0andy<0
(iv) If xy<0, then x<0andy<0
(v) If x<−5andx<−2, than x∈(−∞,−5)
(vi) If x<−5andx>2, then x∈(−5,2)
(vii) If x>−2andx<9,then x∈(−2,9)
(viii) If |x|>5, then x∈(−∞,−5)∪[5,∞)
(ix) If |x|≤4, then x∈[−4,4]
(x)Graph of x<3is
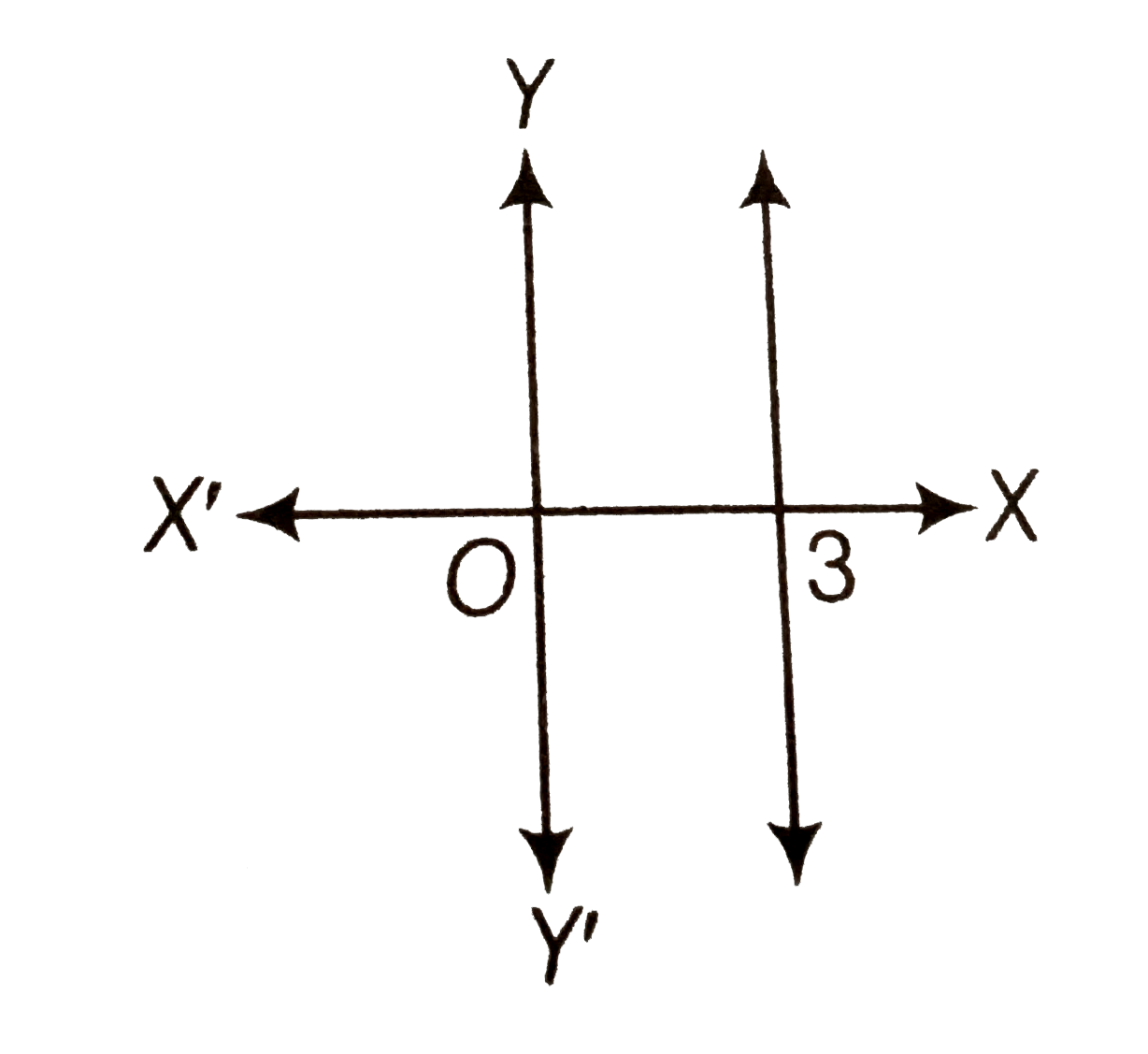
(xi) Graph of x≥0 is

(xii) Graph of y≤0 is
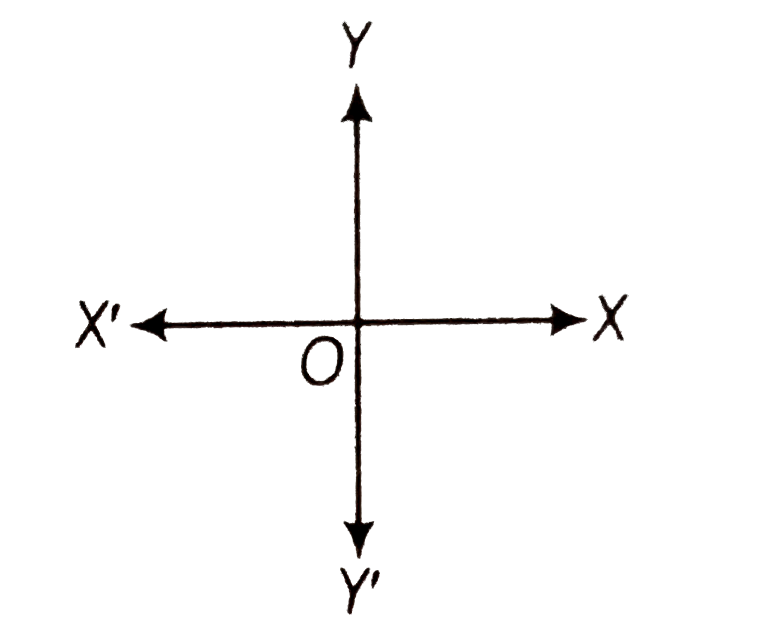
(xiii) Solution set of x≤0andy≤0 is

(xiv) Solution set of x≥0andy≤1 is
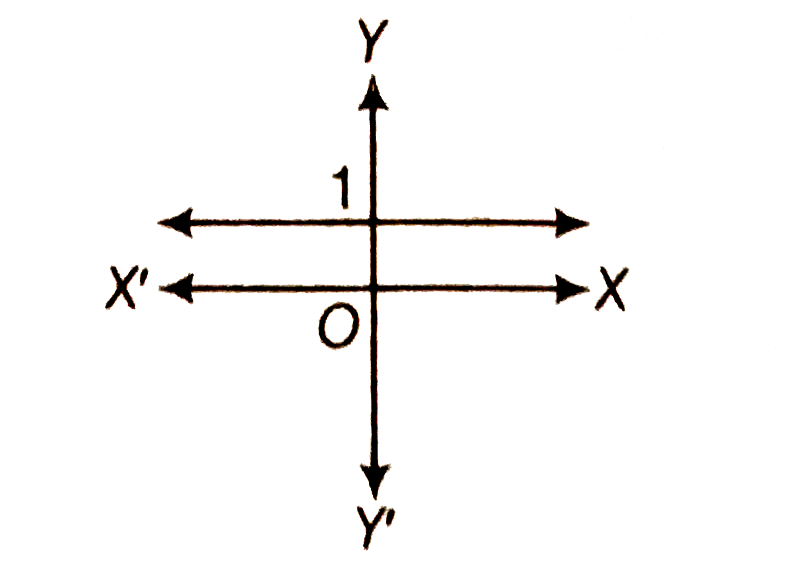
(xv) Solution set of x+y≥0 is
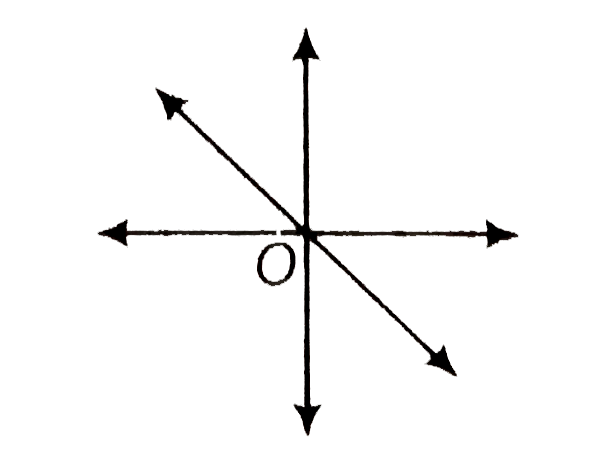
View Solution
Knowledge Check
If byx<0 and bxy<0 then r is _____
Aa<0Bb>0Cc=0Dd>1Let f'(x)>0andg'(x)<0 for all x∈R Then
Af{g(x)>f(g(X+1)}Bf{g(x)>f(g(X−1)}Cg{f(x)>g(f(X+1)}Dg{f(x)>g(f(X−1)}If for a bivariate data, byx=−1.2 and bxy=−0.3 then r =
A−0.06B0.06C0.6D−0.6
State True or False: y=5+2.8x and x=3+0.5y be the regression lines of y on x and x on y respectively ,then byx=−0.5
View SolutionIf a<b and c<0, then ac>bc
View Solutionrxy<0, according as
View SolutionIf a<0andb>0 then the point (a, b) lies in quadrant
View SolutionStatement - 1 : If x>1 then log10x<log3x<logex<log2x.
Statement - 2 : If 0<x<1, then logxa>logxb⇒a<b.
View Solution

