Find potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
Consider a elemental ring of radius r and thickness dr on surface of disc as shown in figure
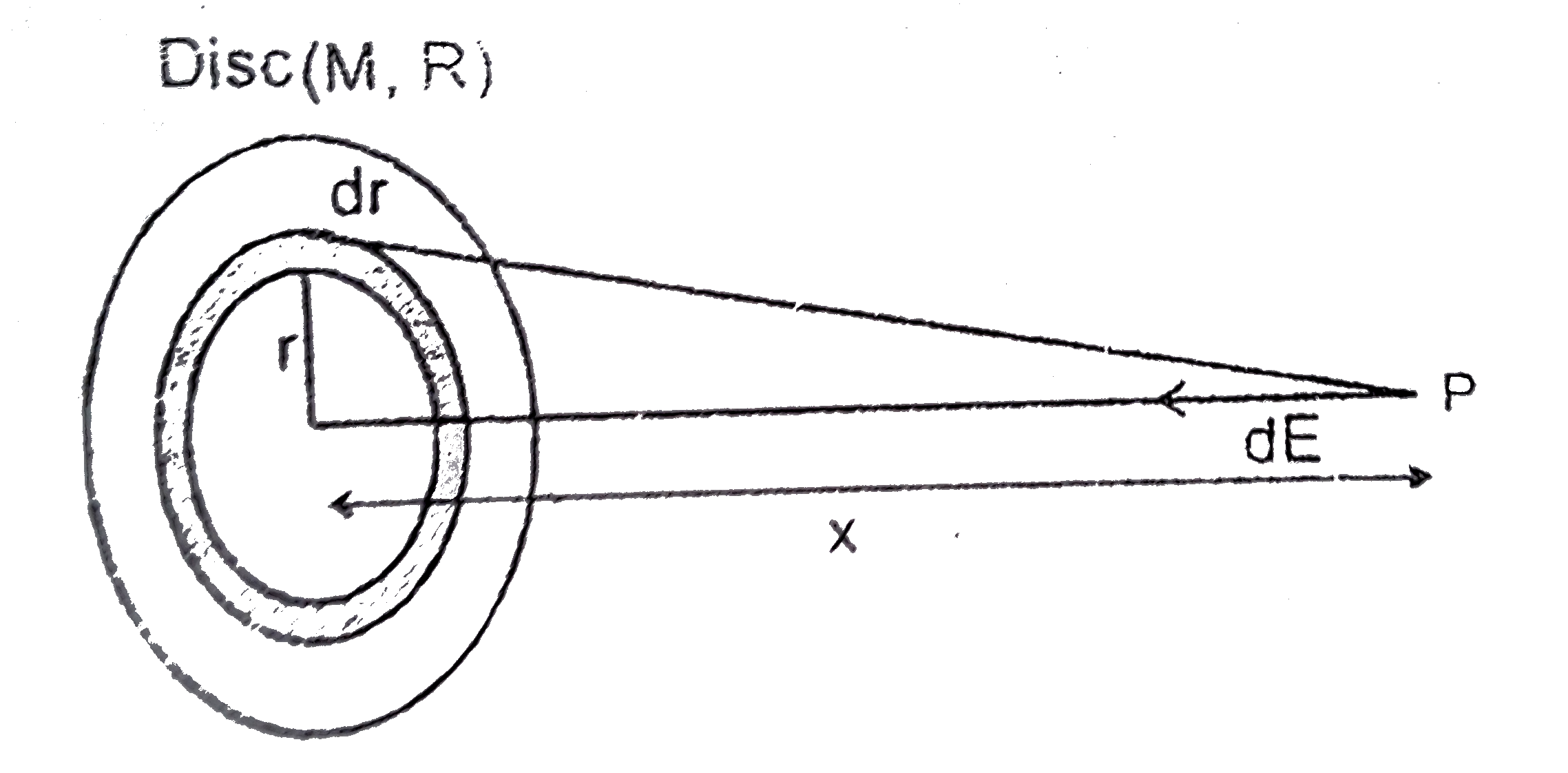
Gravitational field due to elemental ring
dE=GdMx(x2+r2)3/2 Here dM=MπR2.2πrdr=2MR2rdr
∴dE=G.2MxrdxR2(x2+r2)3/2
∴E=R∫0(2GMxR2)rdr(x2+r2)3/2
∴E=2GMxR2[1x−1√x2+R2]
Topper's Solved these Questions
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - SOLVED MISCELLANEOUS PROBLEMS
5 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXAMPLE
2 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- NUCLEAR PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions
16 Videos
Similar Questions
For a uniform ring of mass M and radius R at its centre
View SolutionFind the moment of inertia of a uniform ring of mass M and radius R about a diameter.
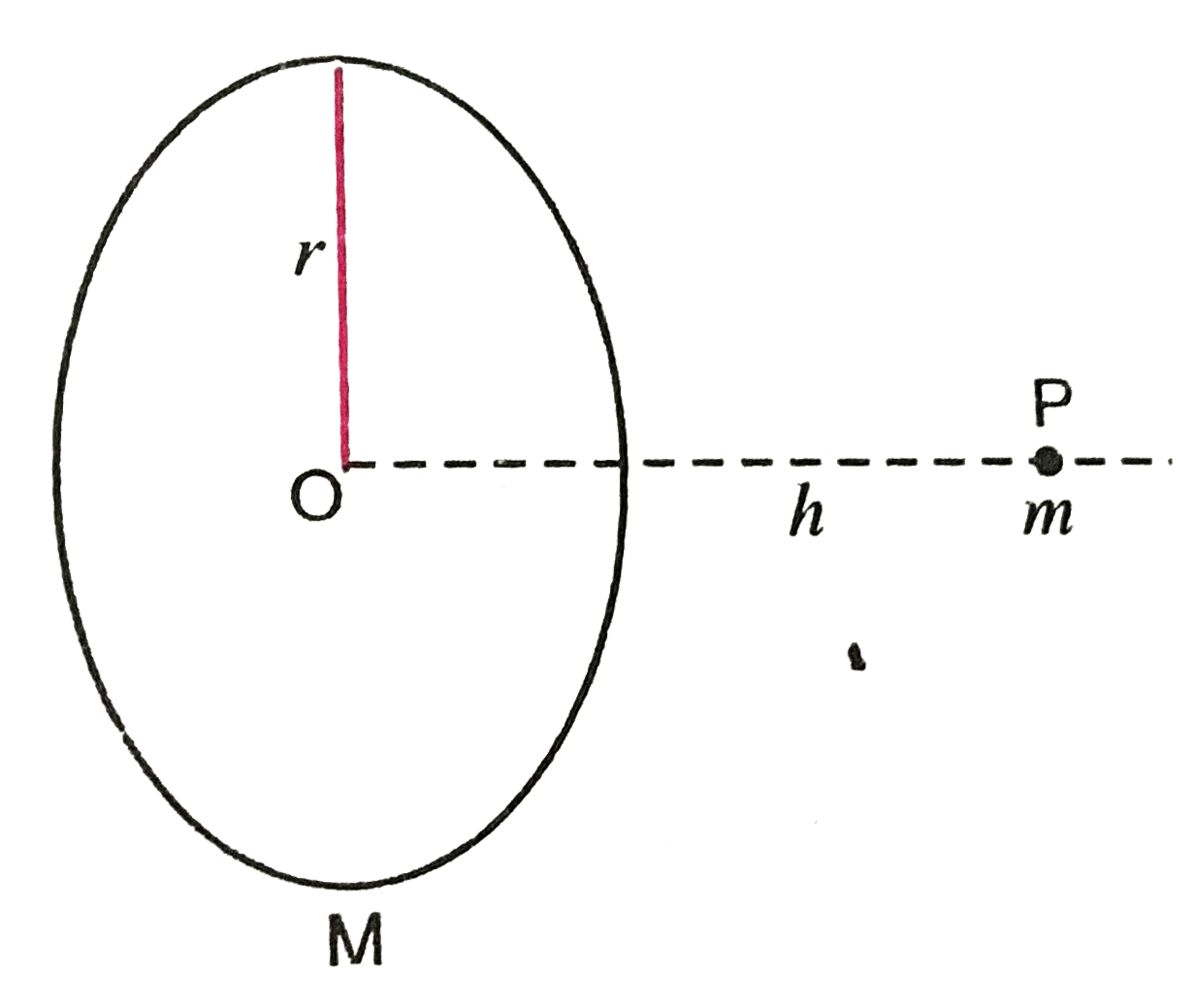
View SolutionA mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig.
If the mass is removed futher away such that OP becomes 2h, by what factor the force of gravitational will decrease, if h=r ?
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View SolutionA particle of mass 1kg is placed at a distance of 4m from the centre and on the axis of a uniform ring mass 5kg and radius 3m. The work done to increase the distance of the particle from 4m to 3√3m is
View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionWhat is the distance of centre of mass of a half fring from centre if the ring has radius =0.5 m [XI]
View Solution
