A flat circular fixed disc has charge +Q uniformly distributed on the disc. A charge +q is thrown with kinetic energy K, towards the disc along its axis. The charge q :
may hit the disc at the centre
may return back along its path after touching the disc
may return back along its path without touching the disc
any of the above three situations is possible depending on the magnitude of K
The correct Answer is:D
To solve the problem, we need to analyze the situation involving a flat circular disc with a uniform charge distribution and a charge thrown towards it. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a flat circular disc with a total charge +Q uniformly distributed over its surface. A charge +q is thrown towards the disc with an initial kinetic energy K. We need to determine the possible outcomes of this interaction.
Step 2: Identify Forces Acting on Charge +q
As the charge +q approaches the disc, it experiences an electrostatic force due to the electric field created by the charged disc. The direction of this force will be opposite to the direction of motion of charge +q (since both charges are positive).
Step 3: Calculate the Electric Field at a Distance x
The electric field E at a distance x from the center of the disc can be derived from the surface charge density σ (where σ=QπR2 for a disc of radius R). The electric field due to a uniformly charged disc along its axis is given by:
Ex=14πϵ0⋅Q(x2+R2)3/2⋅(R2+x2)
This field acts in the direction opposite to the motion of +q.
Step 4: Analyze the Kinetic Energy
The initial kinetic energy K of the charge +q is given by:
K=12mv2
where m is the mass of charge +q and v is its velocity. As the charge moves towards the disc, it will lose kinetic energy due to the work done against the electric field.
Step 5: Determine Possible Outcomes
1. Charge Hits the Disc: If the initial kinetic energy K is sufficiently large, the charge +q can overcome the electric field's retarding force and hit the disc at its center.
2. Charge Returns After Touching: If K is just enough to reach the center but not enough to overcome the electric field's force after touching the disc, the charge may return back along its path after making contact.
3. Charge Returns Without Touching: If K is too small, the charge +q may not reach the disc and will return back along its path without touching it.
Step 6: Conclusion
The outcome of the interaction depends on the magnitude of the initial kinetic energy K given to the charge +q. Therefore, the correct answer is that any of the above three situations is possible depending on the magnitude of K.
Final Answer
D) Any of the above three situations is possible depending on the magnitude of K.
We have a flat circular disc with a total charge +Q uniformly distributed over its surface. A charge +q is thrown towards the disc with an initial kinetic energy K. We need to determine the possible outcomes of this interaction.
As the charge +q approaches the disc, it experiences an electrostatic force due to the electric field created by the charged disc. The direction of this force will be opposite to the direction of motion of charge +q (since both charges are positive).
The electric field E at a distance x from the center of the disc can be derived from the surface charge density σ (where σ=QπR2 for a disc of radius R). The electric field due to a uniformly charged disc along its axis is given by:
Ex=14πϵ0⋅Q(x2+R2)3/2⋅(R2+x2)
This field acts in the direction opposite to the motion of +q.
The initial kinetic energy K of the charge +q is given by:
K=12mv2
where m is the mass of charge +q and v is its velocity. As the charge moves towards the disc, it will lose kinetic energy due to the work done against the electric field.
1. Charge Hits the Disc: If the initial kinetic energy K is sufficiently large, the charge +q can overcome the electric field's retarding force and hit the disc at its center.
2. Charge Returns After Touching: If K is just enough to reach the center but not enough to overcome the electric field's force after touching the disc, the charge may return back along its path after making contact.
The outcome of the interaction depends on the magnitude of the initial kinetic energy K given to the charge +q. Therefore, the correct answer is that any of the above three situations is possible depending on the magnitude of K.
D) Any of the above three situations is possible depending on the magnitude of K.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II Section (C)
Explore 14 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II Section (D)
Explore 2 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II Section (A)
Explore 4 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A plastic disc of radius 'R' has a charge 'q ' uniformly distributed over its surface. If the disc is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge -Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionA thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
View SolutionA sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
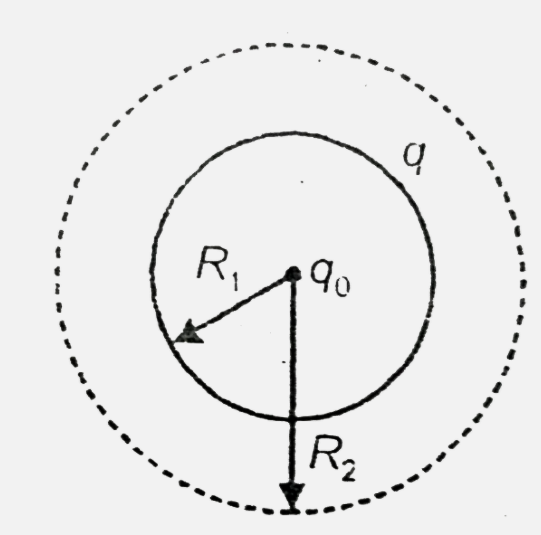
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
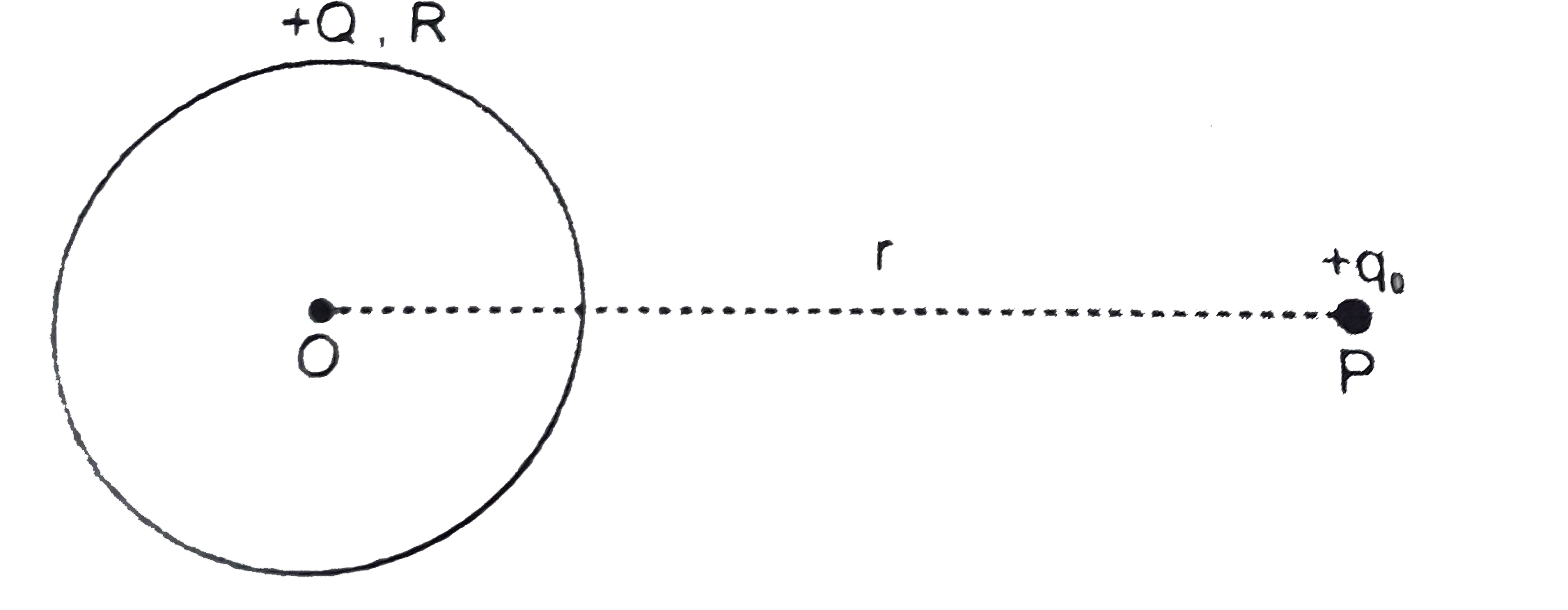
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View Solution

