Two charges ±10μC are placed 5×10−3m apart. Determine the electric field at a point Q,0⋅15m away from O, on a line passing through O and normal to the axis of the dipole.
To solve the problem, we need to determine the electric field at point Q, which is located 0.15 m away from the midpoint O of the dipole consisting of two charges of +10 µC and -10 µC, separated by a distance of 5 mm (5 x 10^(-3) m).
1. Identify the Given Values:
- Charge, Q=10μC=10×10−6C
- Distance between charges, A=5×10−3m
- Distance from the midpoint O to point Q, r=0.15m=15×10−2m
2. Calculate the Dipole Moment (p):
The dipole moment p is given by the formula:
p=Q×A
Substituting the values:
p=(10×10−6C)×(5×10−3m)=5×10−8C⋅m
3. Use the Formula for Electric Field (E) at a Point on the Equatorial Plane:
The electric field E at a distance r from the dipole along the perpendicular bisector (equatorial plane) is given by:
E=k⋅pr3
where k is Coulomb's constant, k=9×109N⋅m2/C2.
4. Substitute the Values into the Electric Field Formula:
E=(9×109)⋅(5×10−8)(0.15)3
5. Calculate (0.15)3:
(0.15)3=0.003375m3
6. Substitute and Simplify:
E=(9×109)⋅(5×10−8)0.003375
E=45×1010.003375
E=45000.003375≈1.33×106N/C
7. Final Result:
The electric field at point Q is approximately:
E≈1.33×105N/C
- Charge, Q=10μC=10×10−6C
- Distance between charges, A=5×10−3m
- Distance from the midpoint O to point Q, r=0.15m=15×10−2m
The dipole moment p is given by the formula:
p=Q×A
Substituting the values:
p=(10×10−6C)×(5×10−3m)=5×10−8C⋅m
The electric field E at a distance r from the dipole along the perpendicular bisector (equatorial plane) is given by:
E=k⋅pr3
where k is Coulomb's constant, k=9×109N⋅m2/C2.
E=(9×109)⋅(5×10−8)(0.15)3
(0.15)3=0.003375m3
E=(9×109)⋅(5×10−8)0.003375
E=45×1010.003375
E=45000.003375≈1.33×106N/C
The electric field at point Q is approximately:
E≈1.33×105N/C
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Two charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
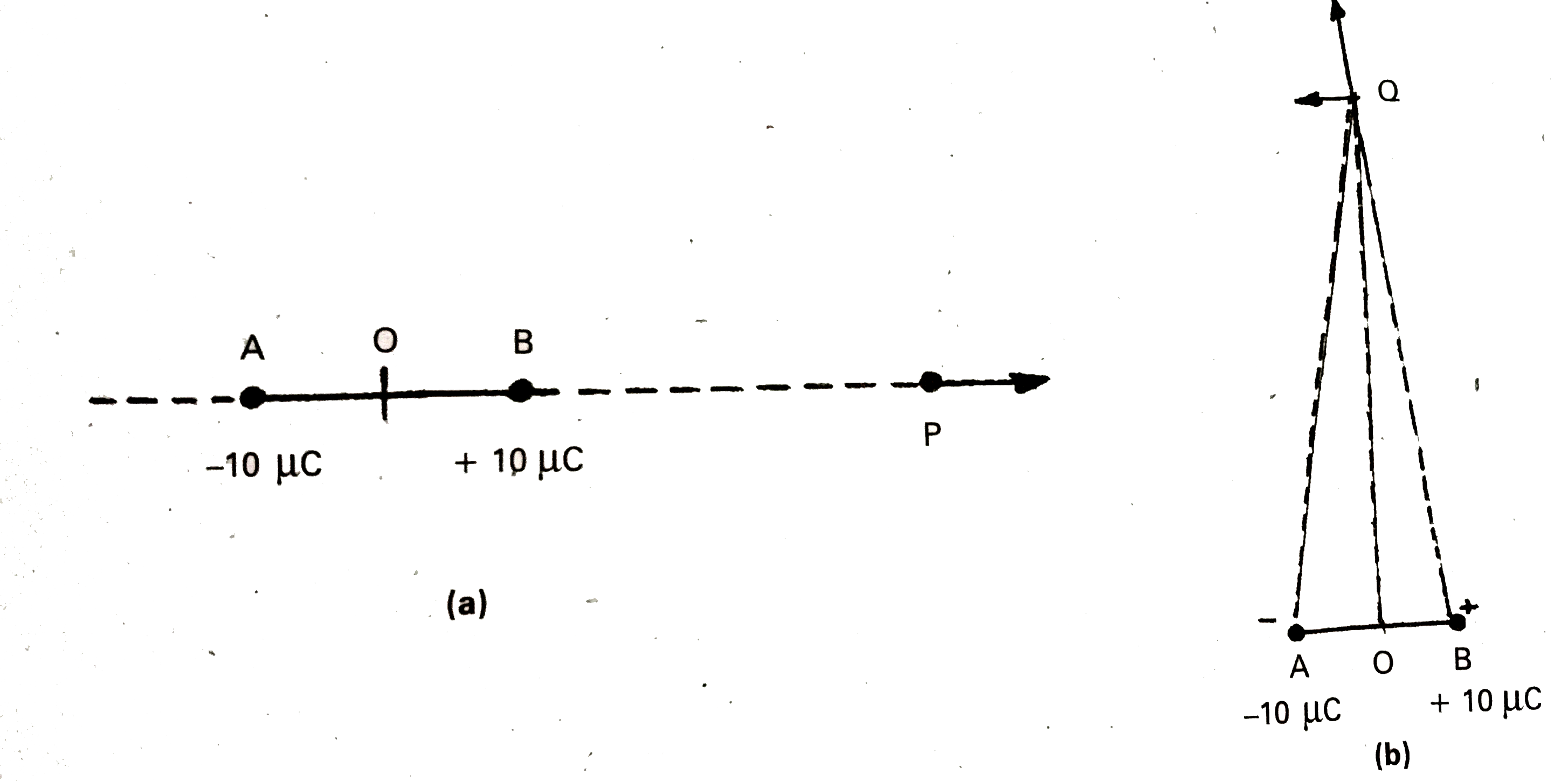
View SolutionTwo charges ±10μC are placed 5⋅0mm apart. Determine the electric field at (a) point P on the axis of dipole 15cm away from its center on the side of the positive charge. As shown in Figure and at (b) a point Q. 15cm away form O on a line passing through O and a line passing through O and normal to the axis of the dipole as shown in Fig.

View SolutionTwo charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
View SolutionTwo charges 4q and q are placed 30 cm. apart. At what point the value of electric field will be zero
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
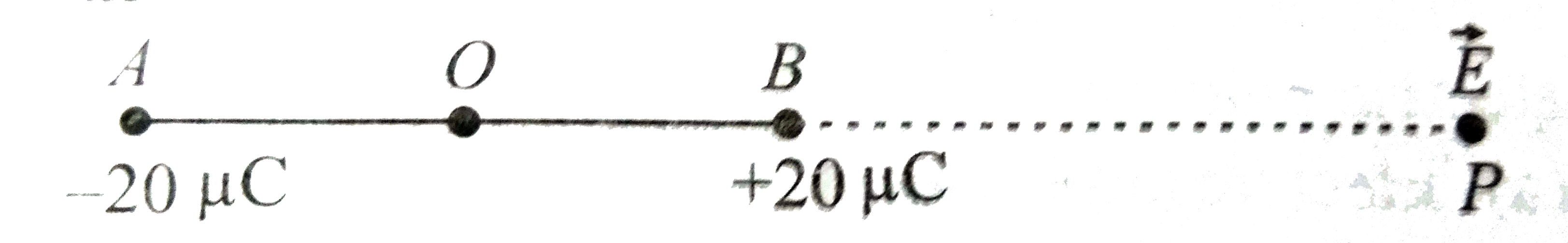
View SolutionA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
View SolutionTwo charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionTwo charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
View Solution

