Two charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
To solve the problem of finding the electric field on the axial and equatorial lines of a dipole consisting of charges +20 µC and -20 µC separated by 5 mm, we can follow these steps:
Step 1: Understand the Dipole Configuration
We have two charges:
- q1=+20μC=20×10−6C
- q2=−20μC=−20×10−6C
The distance between the charges is given as 2a=5mm=5×10−3m. Therefore, the separation a is:
a=5×10−32=2.5×10−3m
Step 2: Calculate the Dipole Moment
The dipole moment P is given by the product of the charge and the separation distance:
P=q⋅2a=(20×10−6)⋅(5×10−3)=100×10−9C⋅m=1×10−7C⋅m
Step 3: Calculate the Electric Field on the Equatorial Line
The formula for the electric field Eequatorial at a distance r from the midpoint of the dipole is:
Eequatorial=14πϵ0⋅Pr3
Given that r=20cm=0.2m and using ϵ0=8.85×10−12C2/(N⋅m2):
Eequatorial=9×109(0.2)3⋅(1×10−7)
Calculating (0.2)3:
(0.2)3=0.008m3
Now substituting:
Eequatorial=9×109⋅1×10−70.008=9×1020.008=112.5×103N/C=1.125×105N/C
Step 4: Calculate the Electric Field on the Axial Line
The relationship between the electric field on the axial line Eaxial and the electric field on the equatorial line is:
Eaxial=2⋅Eequatorial
Substituting the value of Eequatorial:
Eaxial=2⋅1.125×105=2.25×105N/C
Final Results
- Electric field on the equatorial line: Eequatorial=1.125×105N/C
- Electric field on the axial line: Eaxial=2.25×105N/C
We have two charges:
- q1=+20μC=20×10−6C
- q2=−20μC=−20×10−6C
The distance between the charges is given as 2a=5mm=5×10−3m. Therefore, the separation a is:
a=5×10−32=2.5×10−3m
The dipole moment P is given by the product of the charge and the separation distance:
P=q⋅2a=(20×10−6)⋅(5×10−3)=100×10−9C⋅m=1×10−7C⋅m
The formula for the electric field Eequatorial at a distance r from the midpoint of the dipole is:
Eequatorial=14πϵ0⋅Pr3
Given that r=20cm=0.2m and using ϵ0=8.85×10−12C2/(N⋅m2):
Eequatorial=9×109(0.2)3⋅(1×10−7)
Calculating (0.2)3:
(0.2)3=0.008m3
Now substituting:
Eequatorial=9×109⋅1×10−70.008=9×1020.008=112.5×103N/C=1.125×105N/C
The relationship between the electric field on the axial line Eaxial and the electric field on the equatorial line is:
Eaxial=2⋅Eequatorial
Substituting the value of Eequatorial:
Eaxial=2⋅1.125×105=2.25×105N/C
- Electric field on the equatorial line: Eequatorial=1.125×105N/C
- Electric field on the axial line: Eaxial=2.25×105N/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 33 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:ASSIGNMENT(SECTION-A) Objective Type Question
Explore 45 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
Two charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionTwo charges, each of 5μC but opposite in sign, are placed 4 cm apart. Calculate the electric field intensity of a point that is a distance 4 cm from the mid point on the axial line of the dipole.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
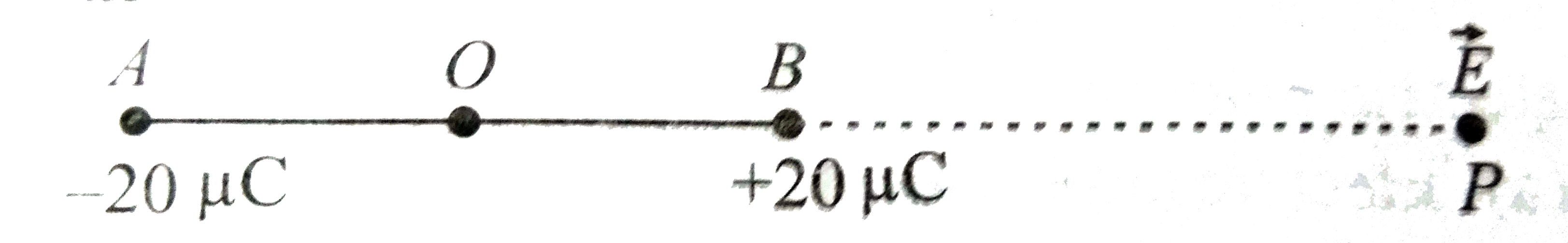
View Solutionfind the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionTwo point charges of 20μC and 80μC are 10 cm apart where will the electric field strength be zero on the line joining the charges from 20μC charge
View SolutionTwo opposite charges each of magnitude 2μC are 1 cm apart. Find electric field at a distance of 5 cm from the min-point on axid line of the dipole. Also, find the field on equatorial line at the same distance from mid-point
View SolutionTwo charges of +25×10−9 coulomb and −25×10−9 coulomb are placed 6 m apart. Find the electric field intensity ratio at points 4 m from the centre of the electric dipole (i) on axial line (ii) on equatorial line
View SolutionTwo charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
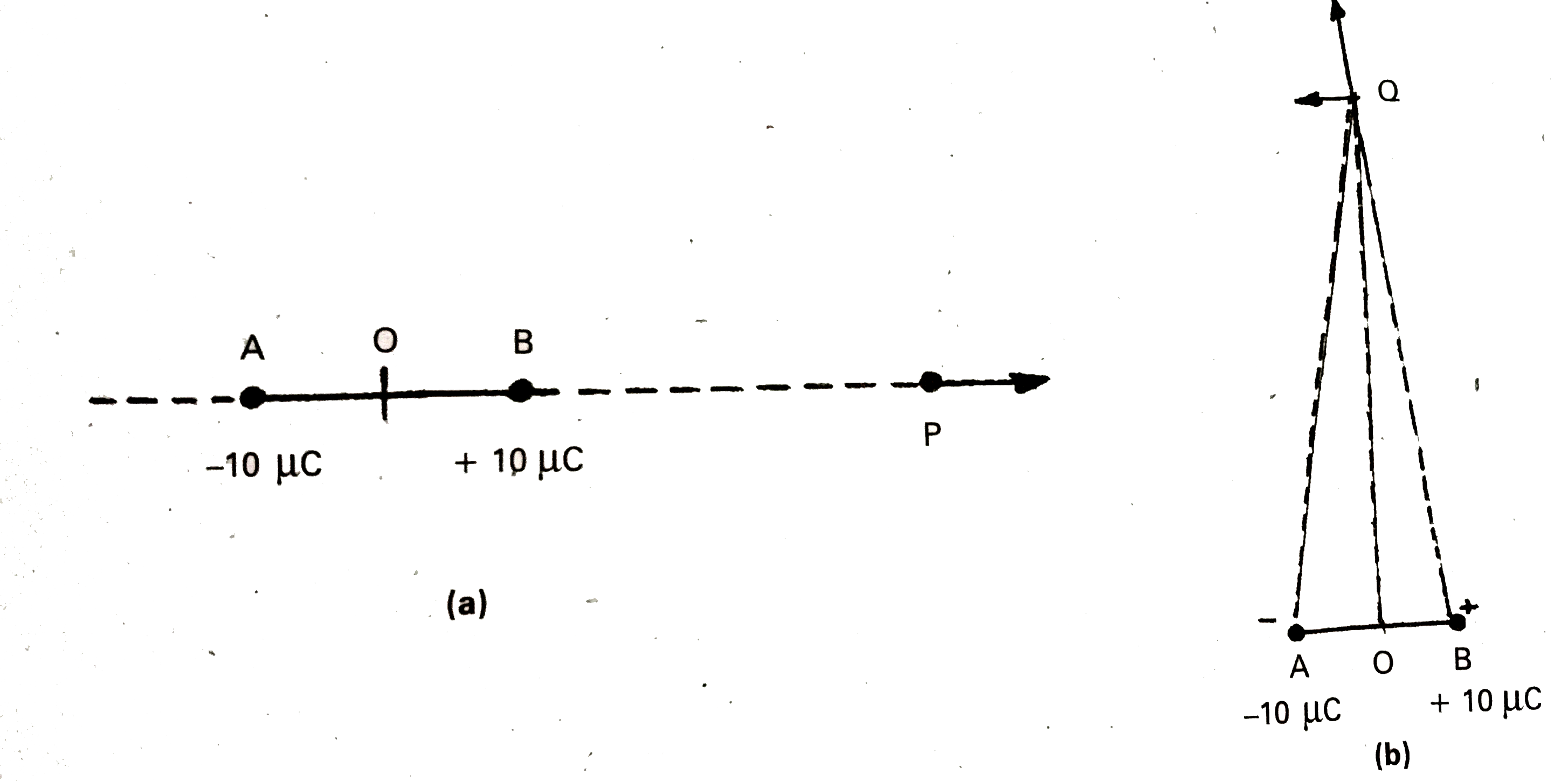
View SolutionTwo charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
View SolutionTwo charges +10μC and +20μC are placed at a. separation of 2 cm. Find the electric potential due to the. pair at the middle point of the line joining the two charges.
View Solution