Two charges +10μC and +20μC are placed at a. separation of 2 cm. Find the electric potential due to the. pair at the middle point of the line joining the two charges.
To find the electric potential at the midpoint between two charges of +10μC and +20μC separated by a distance of 2cm, we can follow these steps:
Step 1: Identify the charges and their positions
We have:
- Charge Q1=+10μC=10×10−6C
- Charge Q2=+20μC=20×10−6C
- Distance between the charges d=2cm=0.02m
Step 2: Determine the distance from the midpoint to each charge
The midpoint between the two charges is at a distance of:
- r1=r2=d2=2cm2=1cm=0.01m
Step 3: Use the formula for electric potential
The electric potential V at a point due to a charge is given by the formula:
V=kQr
where k is Coulomb's constant, k=9×109N⋅m2/C2.
Step 4: Calculate the potential due to each charge at the midpoint
The total electric potential V at the midpoint is the sum of the potentials due to each charge:
V=V1+V2
Where:
- V1=kQ1r1
- V2=kQ2r2
Substituting the values:
V1=9×10910×10−60.01
V2=9×10920×10−60.01
Step 5: Calculate V1 and V2
Calculating V1:
V1=9×109×10×10−60.01=9×109×10−4=9×105V
Calculating V2:
V2=9×109×20×10−60.01=9×109×2×10−4=18×105V
Step 6: Find the total potential
Now, adding V1 and V2:
V=V1+V2=9×105+18×105=27×105V
V=2.7×106V
Final Answer
The electric potential at the midpoint between the two charges is:
V=2.7×106V
We have:
- Charge Q1=+10μC=10×10−6C
- Charge Q2=+20μC=20×10−6C
- Distance between the charges d=2cm=0.02m
The midpoint between the two charges is at a distance of:
- r1=r2=d2=2cm2=1cm=0.01m
The electric potential V at a point due to a charge is given by the formula:
V=kQr
where k is Coulomb's constant, k=9×109N⋅m2/C2.
The total electric potential V at the midpoint is the sum of the potentials due to each charge:
V=V1+V2
Where:
- V1=kQ1r1
- V2=kQ2r2
V1=9×10910×10−60.01
V2=9×10920×10−60.01
Calculating V1:
V1=9×109×10×10−60.01=9×109×10−4=9×105V
V2=9×109×20×10−60.01=9×109×2×10−4=18×105V
Now, adding V1 and V2:
V=V1+V2=9×105+18×105=27×105V
V=2.7×106V
The electric potential at the midpoint between the two charges is:
V=2.7×106V
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Two point charges qA=3μC and qB=−3μC are located 20 cm apart in vaccum (a) what is the electric field at the mid point O of the line AB joining the two charges ? (b) If a negative test charge of magnitude 1.5×10−9C is placed at the point, what is the force experienced by the test charge ?
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.

View Solution
Knowledge Check
Two tiny spheres carrying charges 1.8μCand2.8μC are located at 40 cm apart. The potential at the mid-point of the line joining the two charges is
A3.8×104VB2.1×105VC4.3×104VD6.3×105V
Two tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric. field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View SolutionTwo point charges Q1=400μCand Q2=100μC are kept fixed, 60 cm apart in vacuum. Find intensity of the electric field at midpoint of the line joining Q1 and Q2.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
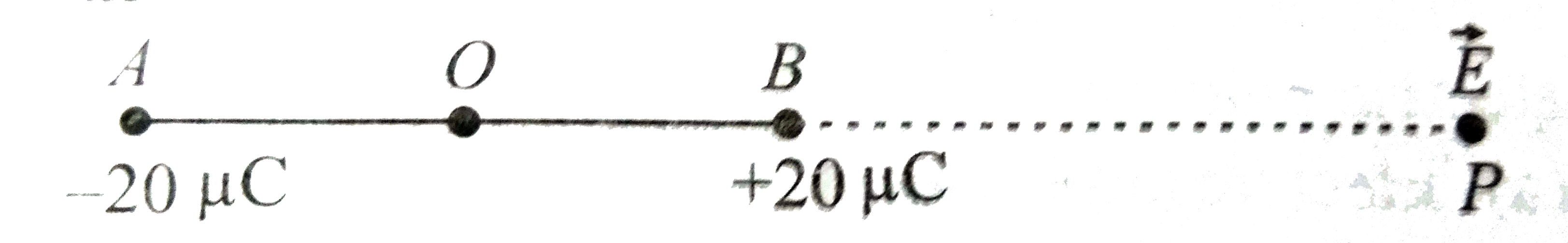
View SolutionTwo charges +20μC and −20μC are 5 mm apart. Find the electric field on axial as well as on the equatorial line at a distance 20 cm from the mid -point of the dipole.
View SolutionTwo spheres A and B are charged with the charges of +10 and +20 coulomb respectively and separated by a distance of 80 cm. The electric field at point on the line joining the centres of the two spheres will be zero at a distance from the sphere A :
View SolutionTwo charges 10μC are placed 5.0 mm apart. Determine the electric field at a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig.
View Solution
