A thin fixed ring of radius a has a positive charge q uniformly distributed over it.A particle of mass m having a negative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively charged particle is approximately simple harmonic. Calculate the time period of oscillation.

When the negative charge is shifted at a distance x from the centre of the ring along its axis then force acting on the point charge due to the ring :
FE=qE (towards centre) =q[Kqy(a2+y2)3/2]
If a>>y then a2+y2≅a2
∴FE=14πε0Qqya3 (Towards centre)
Since, restoring force FE∝y, therefore motion of charge the particle will be S.H.M. Time period of SHM
T=2π√mk=2π
⎷mQq4πε0a3=[16π3ε0ma3Qq]1/2
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.

View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionA charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
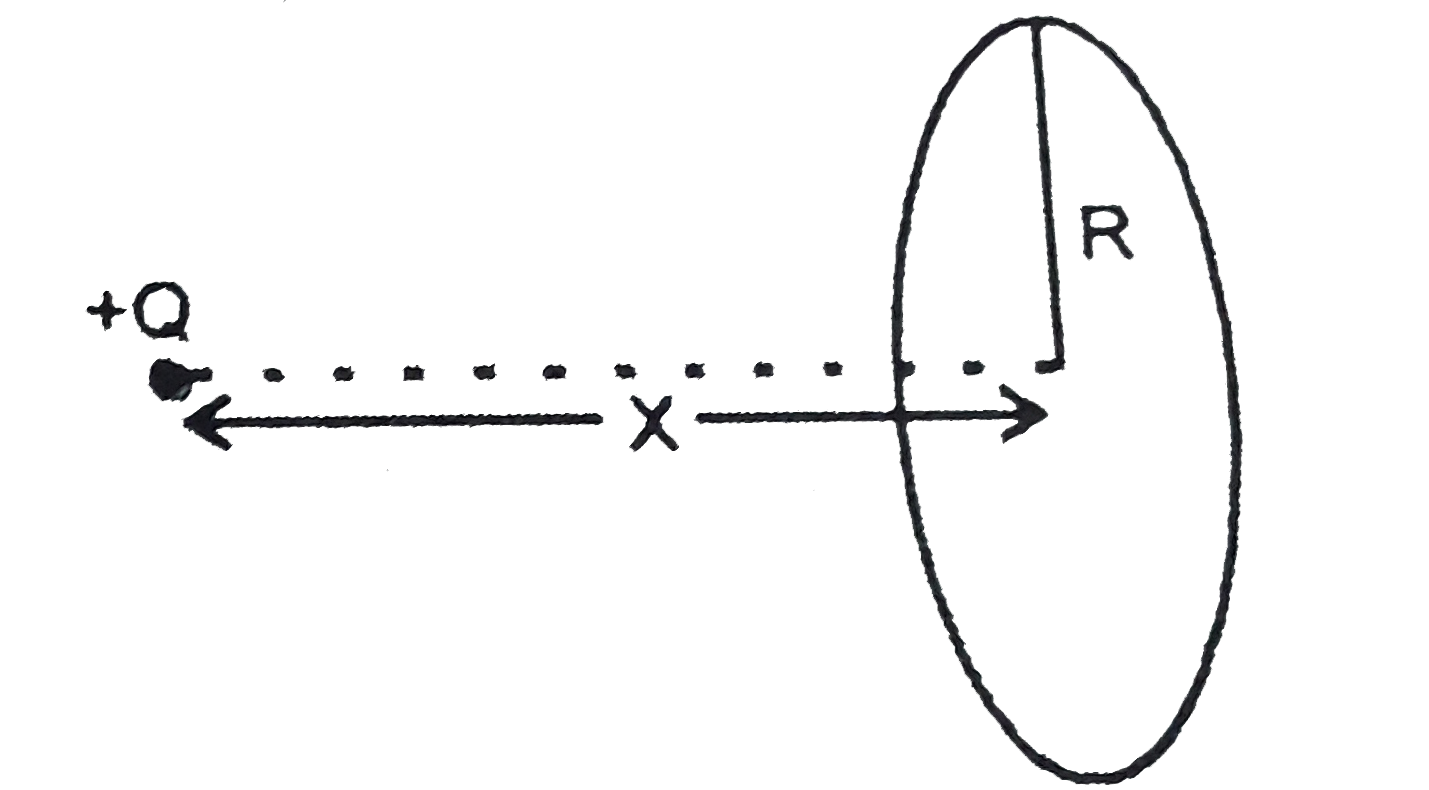
View SolutionA charge +Q is uniformly distributed over a thin ring with radius R. A negative point charge −Q and mass m starts from rest at a point far away from the centre of the ring and moves towards the centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View Solution