Square packed sheets are arranged on the top fo the other such that a sphere in the next layer rests on the center of a square in the previous layer. Identify the type of arrangement and find the coordination number:
Simple Cubic, 6
Face centered cubic, 8
Face centered cubic 12
Body centered cubic, 8
The correct Answer is:C
To solve the problem, we need to identify the type of arrangement of spheres in the given scenario and determine the coordination number.
1. Understanding the Arrangement:
- The problem states that square-packed sheets are arranged on top of each other.
- A sphere in the next layer rests on the center of a square in the previous layer.
2. Identifying the Layers:
- Let's denote the first layer as Layer A and the second layer as Layer B.
- The arrangement is such that Layer B is positioned directly above Layer A, with spheres in Layer B resting on the centers of the squares formed by the spheres in Layer A.
3. Recognizing the Pattern:
- The arrangement alternates between layers: Layer A, Layer B, Layer A, and so on.
- This type of stacking is characteristic of an AB AB arrangement.
4. Determining the Type of Arrangement:
- The AB AB arrangement corresponds to a body-centered cubic (BCC) structure.
- In a BCC structure, there is one atom at the center of the cube and atoms at the corners.
5. Calculating the Coordination Number:
- In a body-centered cubic arrangement, the atom at the center is surrounded by atoms in the adjacent layers.
- Specifically, it is surrounded by four atoms in the layer above and four atoms in the layer below.
- Therefore, the total number of atoms surrounding the central atom is 8.
6. Conclusion:
- The type of arrangement is a body-centered cubic (BCC) arrangement.
- The coordination number for this arrangement is 8.
Final Answer:
- Type of Arrangement: Body-Centered Cubic (BCC)
- Coordination Number: 8
- The problem states that square-packed sheets are arranged on top of each other.
- A sphere in the next layer rests on the center of a square in the previous layer.
- Let's denote the first layer as Layer A and the second layer as Layer B.
- The arrangement is such that Layer B is positioned directly above Layer A, with spheres in Layer B resting on the centers of the squares formed by the spheres in Layer A.
- The arrangement alternates between layers: Layer A, Layer B, Layer A, and so on.
- This type of stacking is characteristic of an AB AB arrangement.
- The AB AB arrangement corresponds to a body-centered cubic (BCC) structure.
- In a BCC structure, there is one atom at the center of the cube and atoms at the corners.
- In a body-centered cubic arrangement, the atom at the center is surrounded by atoms in the adjacent layers.
- Specifically, it is surrounded by four atoms in the layer above and four atoms in the layer below.
- Therefore, the total number of atoms surrounding the central atom is 8.
- The type of arrangement is a body-centered cubic (BCC) arrangement.
- The coordination number for this arrangement is 8.
- Type of Arrangement: Body-Centered Cubic (BCC)
- Coordination Number: 8
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Part-III (Single and double value integer type)
6 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Part-III (One or more than one option correct type)
3 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Part-II National standard examination in chemistry
27 Videos
- S BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - S BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Biomolecules & Polymer)
4 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
In a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The empty space in this hcp unit cell is
(a)74%
(b)48.6%
(c)32%
(d)26%
View SolutionTwo dimensional close packed structure can be generated by stacking the rows of close packed spheres. This can be done in two different ways.
(I) The second row may be placed in contact with the first one, such that the spheres of the second row are exactly above those of first row. The spheres of the two rows are aligned vertically as well as horizontally.
If we call the first row as 'A' type of row, the second row being exactly same as the first one is also of 'A' type. Similarly, we may place more rows to obtain AAAA.... type arrangement
(II) In this type, the second row may be placed above the first one in a staggered manner such that its spheres. fit in depressions of first row. if the arrangement of spheres in the first row is called 'A' type the one in the second row is different and may be called 'B' type. When the third row is placed adjacent to the second in staggered manner, its spheres are aligned with those of first layer. Hence this layer is also 'A' type. The spheres of similarly placed fourth row will be aligned with those of the second row ('B' type). Hence this arrangement is of ABAB.... type
The type of voids generated in type (I) & (II) respectively are
View SolutionPreeti is arranging pencils in a box. If in one layer, she puts in three pencils, then find the rule for the number of pencils in the box if the number of layers in the box is s.
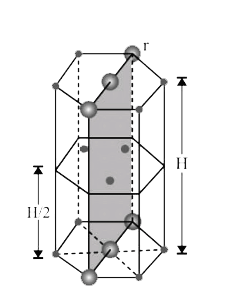
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The volume of this HCP unit cell is

View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The empty space in this HCP unit cell is :
View SolutionWhenever two-demiensional square packing same layers are kept in the way so that the centres are aligned in all three dimensation, coordination numberof each sphere is
View SolutionA metal crystallizes in a closed packed structure, the atoms stack together occupying maximum space and leaving minimum vacant space. Each sphere in the first layer is in contact with six neighbours. Now while arranging the second layer on the first layer, spheres are placed in depression of first layer. Spheres of third layer lie in the depression of second layer.
This repeating arrangement of atoms produces a giant lattice.
If one of the edge length of unit cell is 'a' what is the shortest distance between two atoms?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View Solution
