In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
AB
A3B2
A2B
AB3
The correct Answer is:B
To solve the problem, we need to determine the general formula of the compound formed when anions (A) occupy a hexagonal close packing (HCP) structure and cations (C) occupy only 2/3 of the octahedral voids in that structure. Let's break down the solution step by step.
1. Understanding the HCP Structure:
- In a hexagonal close packing (HCP) arrangement, the coordination number is 12, and the number of spheres (or particles) per unit cell is 6. This means that the effective number of anions (A) in the unit cell is 6.
2. Identifying the Octahedral Voids:
- In HCP, the number of octahedral voids is equal to the number of atoms in the unit cell. Therefore, there are also 6 octahedral voids in the HCP structure.
3. Calculating the Number of Cations (C):
- According to the problem, cations (C) occupy only 2/3 of the octahedral voids.
- Since there are 6 octahedral voids, the number of cations (C) that will occupy these voids is:
Number of C=23×6=4
4. Writing the General Formula:
- Now that we know the number of anions (A) and cations (C) in the unit cell, we can write the general formula.
- The number of A is 6 and the number of C is 4, so the formula can be represented as:
General formula=A6C4
5. Simplifying the Formula:
- To simplify the formula A6C4, we can divide both subscripts by 2:
A6C4→A3C2
Final Answer:
The general formula of the compound is A3C2.
- In a hexagonal close packing (HCP) arrangement, the coordination number is 12, and the number of spheres (or particles) per unit cell is 6. This means that the effective number of anions (A) in the unit cell is 6.
- In HCP, the number of octahedral voids is equal to the number of atoms in the unit cell. Therefore, there are also 6 octahedral voids in the HCP structure.
- According to the problem, cations (C) occupy only 2/3 of the octahedral voids.
- Since there are 6 octahedral voids, the number of cations (C) that will occupy these voids is:
Number of C=23×6=4
- Now that we know the number of anions (A) and cations (C) in the unit cell, we can write the general formula.
- The number of A is 6 and the number of C is 4, so the formula can be represented as:
General formula=A6C4
- To simplify the formula A6C4, we can divide both subscripts by 2:
A6C4→A3C2
The general formula of the compound is A3C2.
Similar Questions
In HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
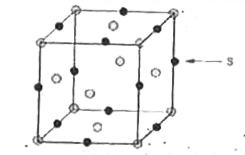
In the figure given below, the site marked as S is a
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
View SolutionIf the radius of the spheres in the close packing is R and the radius pf pctahedral voids is r, then r=0.414R.
View SolutionA compound is formed by cation C and anion A. The anions form hexagonal close packed (hcp) lattice and the cations occupy 75% of octahedral voids. The formula of the compound is
View SolutionIn a crystal of an ionic compound, the ions B form the close packed lattice and the ions A occupy all the tetrahedral voids. The formula of the compound is
View SolutionIn a close packed array of N spheres, the number of tetrahedral holes are
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of the spheres forming closest packing arrangement, then radius r of the octahedral void will be 0.225 R––––––––.
View SolutionCorrect the following statement by changing the underlined part of the sentence.
If R is the radius of spheres forming closest packing arrangement, then radius r of the tetrahedral void will be 0.732R––––––––.
View Solution

