1 mole of an ideal diatomic gas undergoes a reversible polytropic process (PV2=constant). The gas expand from initial volume of 1 litre and temp 300K to final volume 3 lit. Claculate change in internal energy (approx).
−40KJ
−4.2KJ
−4.4KJ
−4.6KJ
The correct Answer is:B
To calculate the change in internal energy (ΔU) for the given process, we can follow these steps:
Step 1: Identify the given data
- Number of moles (n) = 1 mole
- Initial volume (V1) = 1 L = 0.001 m³ (conversion to cubic meters for calculations)
- Final volume (V2) = 3 L = 0.003 m³
- Initial temperature (T1) = 300 K
- For a diatomic gas, the molar heat capacity at constant volume (C_v) = (5/2)R
Step 2: Calculate the final temperature (T2)
Using the relation for a polytropic process, we have:
P1Vn1=P2Vn2
Since PV=nRT, we can express pressure in terms of temperature and volume:
P1=nRT1V1
P2=nRT2V2
Equating the two expressions:
nRT1V1Vn1=nRT2V2Vn2
For a polytropic process where n=2:
T1Vn−11=T2Vn−12
T1V1=T2V2
Now substituting the known values:
300×1=T2×3
T2=3003=100 K
Step 3: Calculate the change in temperature (ΔT)
ΔT=T2−T1=100−300=−200 K
Step 4: Calculate the change in internal energy (ΔU)
Using the formula for change in internal energy:
ΔU=nCvΔT
Where Cv=52R and R=8.314J/mol⋅K:
Cv=52×8.314=20.785J/mol⋅K
Now substituting the values:
ΔU=1×20.785×(−200)
ΔU=−4157J
Final Answer
The change in internal energy (ΔU) is approximately -4157 J.
---
- Number of moles (n) = 1 mole
- Initial volume (V1) = 1 L = 0.001 m³ (conversion to cubic meters for calculations)
- Final volume (V2) = 3 L = 0.003 m³
- Initial temperature (T1) = 300 K
- For a diatomic gas, the molar heat capacity at constant volume (C_v) = (5/2)R
Using the relation for a polytropic process, we have:
P1Vn1=P2Vn2
Since PV=nRT, we can express pressure in terms of temperature and volume:
P1=nRT1V1
P2=nRT2V2
nRT1V1Vn1=nRT2V2Vn2
T1Vn−11=T2Vn−12
T1V1=T2V2
300×1=T2×3
T2=3003=100 K
ΔT=T2−T1=100−300=−200 K
Using the formula for change in internal energy:
ΔU=nCvΔT
Where Cv=52R and R=8.314J/mol⋅K:
Cv=52×8.314=20.785J/mol⋅K
ΔU=1×20.785×(−200)
ΔU=−4157J
The change in internal energy (ΔU) is approximately -4157 J.
Topper's Solved these Questions
- THERMODYNAMICSBook:RESONANCE ENGLISHChapter:THERMODYNAMICSExercise:Exercise -2 Part-I: Only one option correct type
Explore 23 Videos
- THERMODYNAMICSBook:RESONANCE ENGLISHChapter:THERMODYNAMICSExercise:Exercise-2 II: Single and double value integer type
Explore 16 Videos
- THERMODYNAMICSBook:RESONANCE ENGLISHChapter:THERMODYNAMICSExercise:H-1
Explore 1 Video
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:CHEMISTRY
Explore 50 Videos
Similar Questions
2 moles of an ideal monoatomic gas undergo a reversible process for which PV2= constant. The gas sample is made to expand from initial volume of 1 litre of final volume of 3 litre starting from initial temperature of 300 K. find the value of ΔSsys for the above process. Report your answer as Y where ΔSsys=−YRIn3
View Solution2 mole of an ideal monoatomic gas undergoes a reversible process for which PV2=C. The gas is expanded from initial volume of 1 L to final volume of 3 L starting from initial temperature of 300 K. Find ΔH for the process :
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionA diatomic gas undergoes a process represented by PV1.3= constant . Choose the incorrect statement
View SolutionAn ideal monatomic gas undergoes process PV1.25 = constant .Then
View SolutionA gas of volume changes 2 litre to 10 litre at constant temperature 300K, then the change in internal energy will be :
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
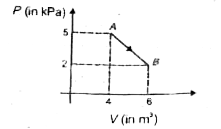
The change to internal energy of the gas during the transition is
View SolutionInitial volume of a gas is 1L at temperature 100K. What is the volume of a gas at 300K.
View SolutionWhat will be the entropy change when two moles of an ideal gas expand reversibly from initial volume of 1 litre to 10 litre at constant temperature of 300 K?
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
(c) the work done by the gas during the process. [ R=8.31J/mol−K]
View Solution