The molar heat capacity for the process shown in fig. is
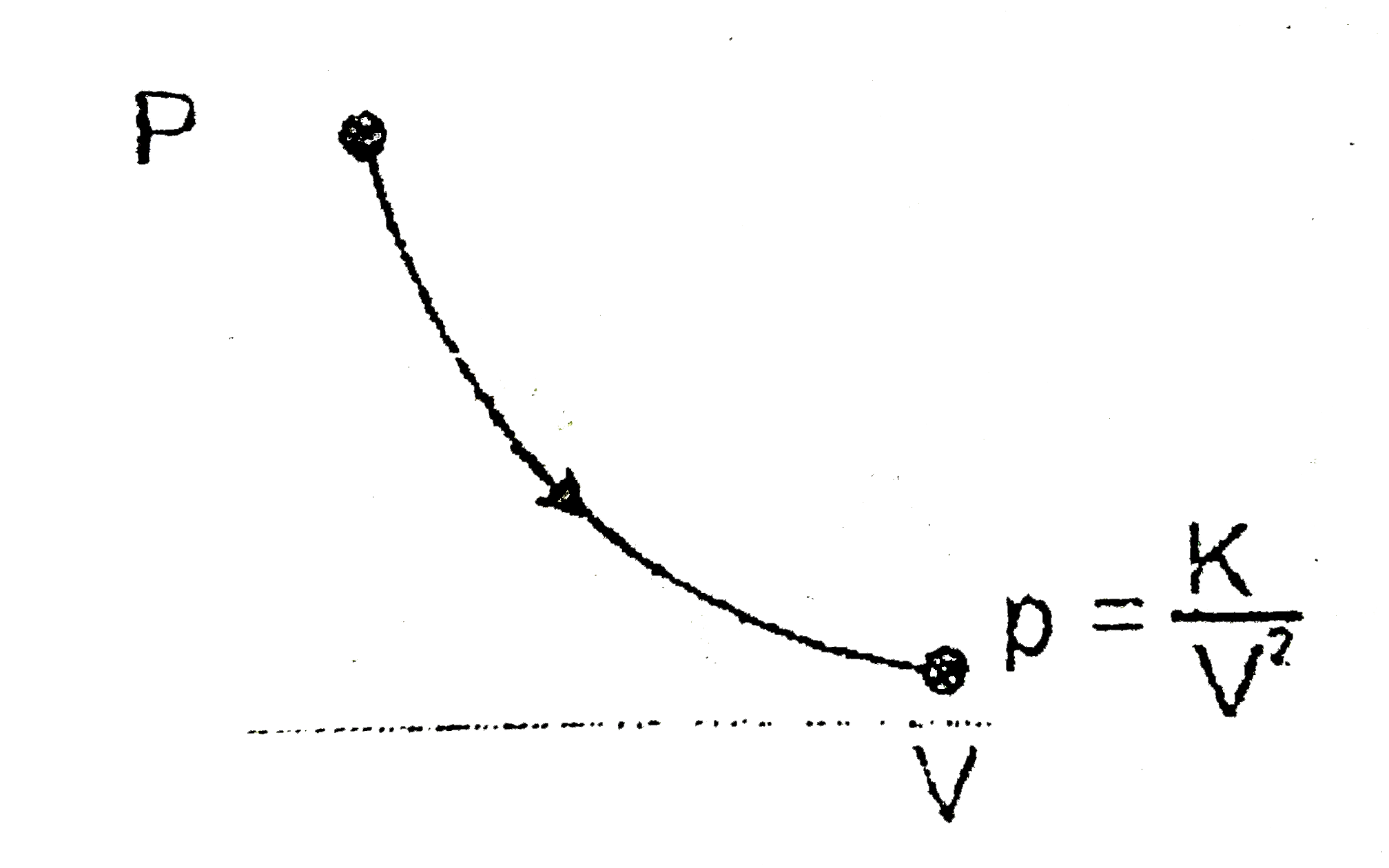
C=Cv
C=Cp
C>Cv
C<Cv
The correct Answer is:D
For polytropic process PVx=k,
C=Cv+R1−x⇒As PV2=K(given) ⇒putx=2
C=Cv+R1−2=Cv−R∴C<Cv
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise -2 Part-I: Only one option correct type
23 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 II: Single and double value integer type
16 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - H-1
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
The molar heat capacity for the process shown in figure is
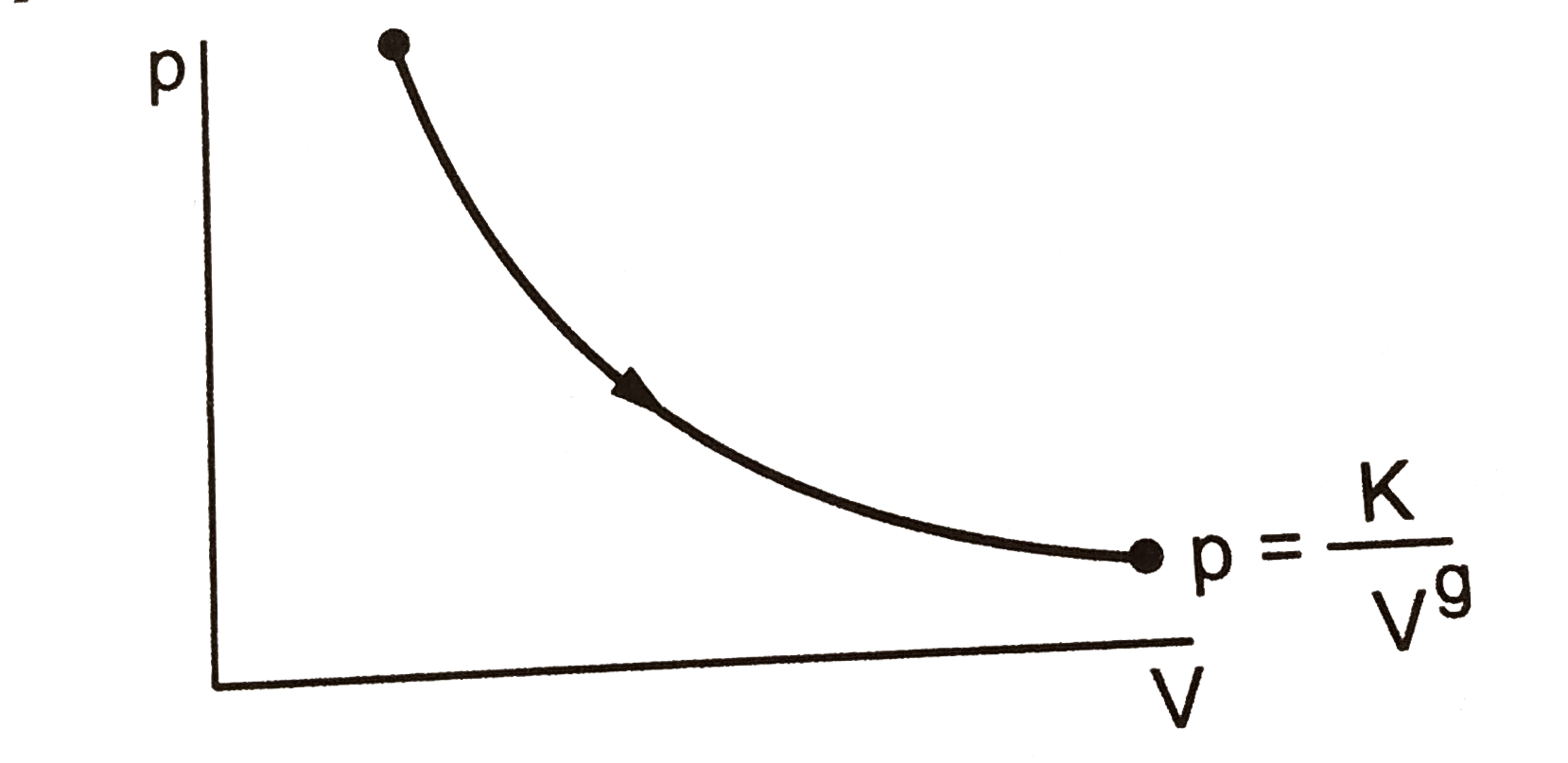
View SolutionThe molar heat capacity for the process shown in fig. is

View SolutionIf molar heat capacity of the given process (as shown in figure) is C, then

View SolutionThe molar heat capacity for an ideal gas
View SolutionA polytropic process for an ideal gas is represented by equation PVn=constant. If g is ratio of specific heats (CpCv), then value of n for which molar heat capacity of the process is negative is given as
View SolutionIf ideal diatomic gas follows the process, as shown in graph, where T is temperature in kelvin and V is volume (m3), then molar heat capacity for this process will be [in terms of gas constant R]:

View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View SolutionThe variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
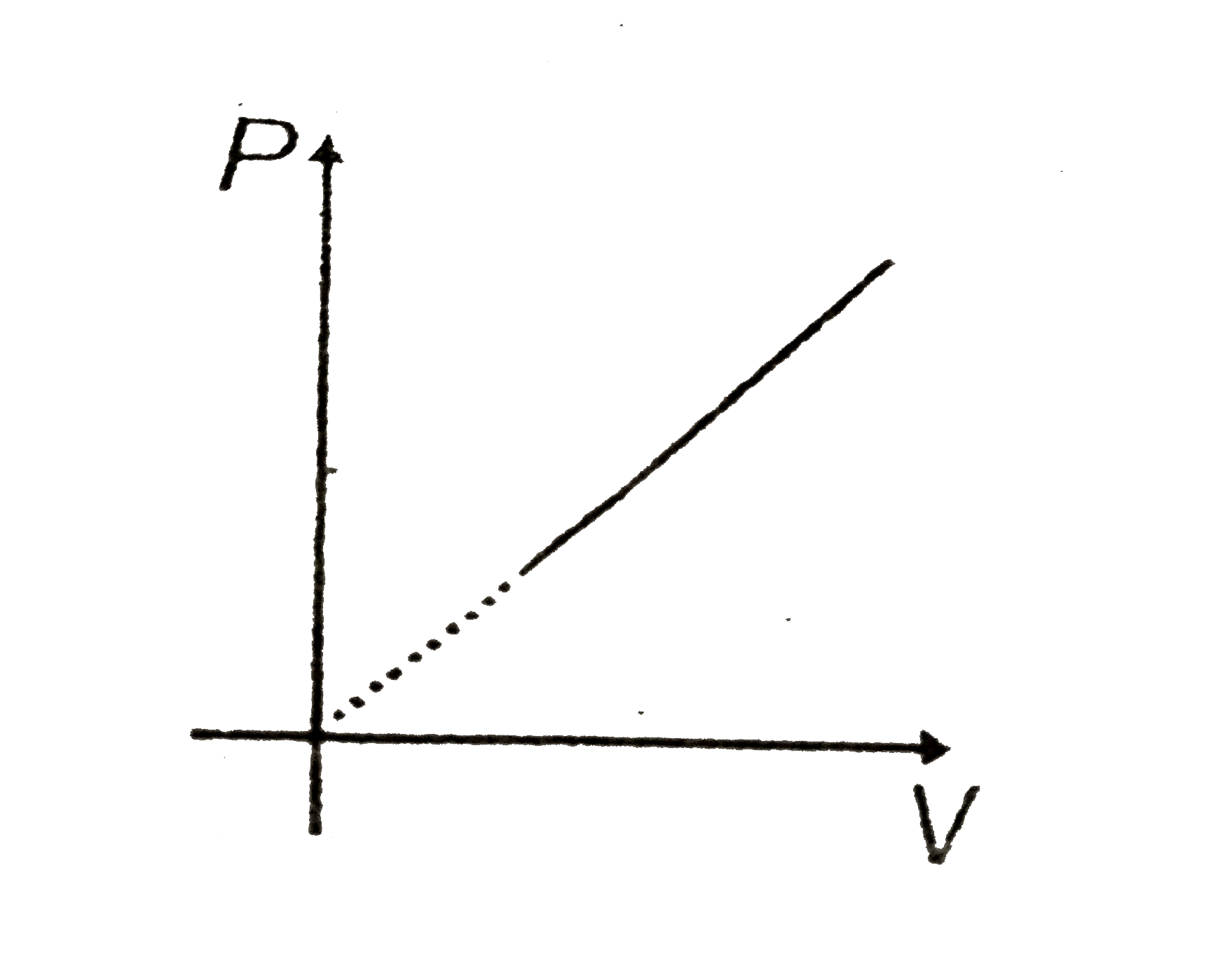 .
.
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
View Solution
