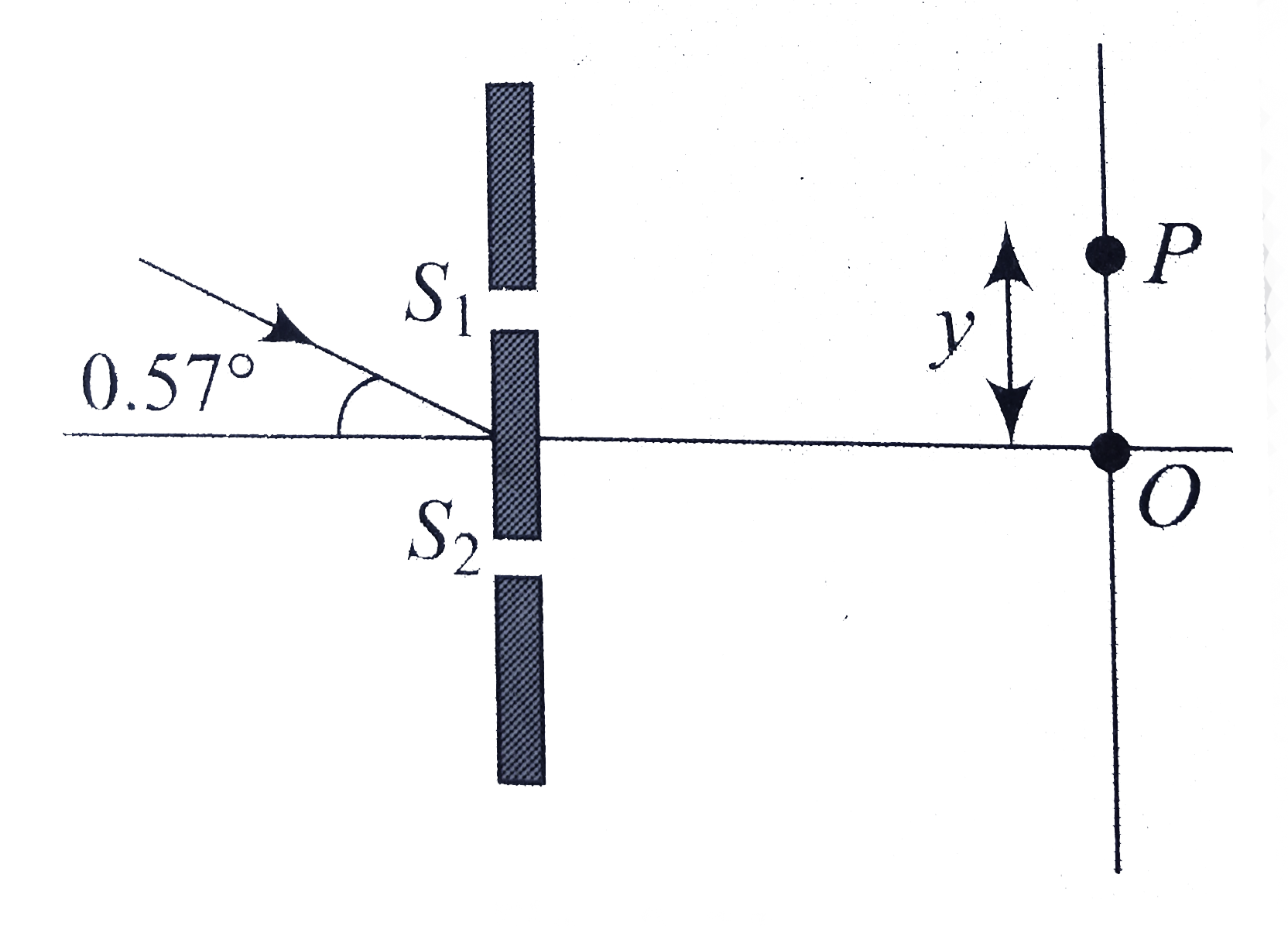
In YDSE with D=1m,d=1mm, light of wavelength 500nm is incident at an angle of 0.57∘ w.r.t. the axis of symmetry of the experimental set-up. If center of symmetry of screen is O as shown figure.
a. find the position of centrla maxima,
b. find intensity at point O in terms of intensity of central maxima I0, and
c. find number of maixma lying central maxima.
 .
.
(i) θ=θ0=0.57∘
⇒y=−Dtanθ≅−Dθ=−1 meter ×(0.5757rad)⇒y=−1cm.
(ii) for point0,θ=0
Hence, Δp=dsinθ0,dthη0=1mm×(10−2rad)
=10,000nm=20×(500nm)
⇒Δp=20λ
Hence point O, corresponds to 20th maxima ⇒ intensity at O=I0
(iii) 19 maxima lie between central maxima and O, excluding maxima at O and central maxima.
Topper's Solved these Questions
Similar Questions
Light of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
View SolutionLight of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is
View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionIn YDSE path difference at a point on screen is λ8 . Find ratio of intensity at this point with maximum intensity.
View SolutionIn YDSE of equal width slits, if intensity at the center of screen is I0, then intensity at a distance of β/4 from the central maxima is
View SolutionA beam of light of wavelength 400 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 2 m away from the slit. It is observed that 2nd order minima occurs at a distance of 2 mm from the position of central maxima. Find the width of the slit.
View SolutionIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionThe diffraction pattern of a single slit is shown in the figure. The point at which the path difference of the extreme rays is two times the wavelength is

View Solution