and are two sources of light which produce individually disturbance at point given by Assume to along the same line, find the resultant after their superposition.
To find the resultant electric field after the superposition of the two disturbances given by E1=3sin(ωt) and E2=4cos(ωt), we can follow these steps:
Step 1: Rewrite E2 in terms of sine
We know that cos(ωt) can be expressed in terms of sine:
E2=4cos(ωt)=4sin(ωt+π2)
This allows us to express both electric fields in terms of sine functions.
Step 2: Identify the amplitudes and phase differences
Now we have:
E1=3sin(ωt)
E2=4sin(ωt+π2)
The phase difference between E1 and E2 is π2.
Step 3: Use the formula for resultant amplitude
The resultant amplitude E can be calculated using the formula:
E2=E21+E22+2E1E2cos(ϕ)
where ϕ is the phase difference. Here, ϕ=π2 and cos(π2)=0.
Step 4: Substitute the values into the formula
Substituting the values:
E2=32+42+2⋅3⋅4⋅cos(π2)
E2=9+16+0
E2=25
Step 5: Calculate the resultant electric field
Taking the square root:
E=√25=5
Step 6: Determine the phase of the resultant
Now, we need to find the phase angle ϕ0 of the resultant electric field. We can use the tangent function:
tan(ϕ0)=E2E1=43
Thus,
ϕ0=tan−1(43)
Step 7: Calculate the angle
Using a calculator or trigonometric tables:
ϕ0≈53∘
Final Result
The resultant electric field can be expressed as:
E=5sin(ωt+53∘)
Summary
The resultant electric field after the superposition of the two disturbances is:
E=5sin(ωt+53∘)
---
We know that cos(ωt) can be expressed in terms of sine:
E2=4cos(ωt)=4sin(ωt+π2)
This allows us to express both electric fields in terms of sine functions.
Now we have:
E1=3sin(ωt)
E2=4sin(ωt+π2)
The phase difference between E1 and E2 is π2.
The resultant amplitude E can be calculated using the formula:
E2=E21+E22+2E1E2cos(ϕ)
where ϕ is the phase difference. Here, ϕ=π2 and cos(π2)=0.
Substituting the values:
E2=32+42+2⋅3⋅4⋅cos(π2)
E2=9+16+0
E2=25
Taking the square root:
E=√25=5
Now, we need to find the phase angle ϕ0 of the resultant electric field. We can use the tangent function:
tan(ϕ0)=E2E1=43
Thus,
ϕ0=tan−1(43)
Using a calculator or trigonometric tables:
ϕ0≈53∘
The resultant electric field can be expressed as:
E=5sin(ωt+53∘)
The resultant electric field after the superposition of the two disturbances is:
E=5sin(ωt+53∘)
Topper's Solved these Questions
Similar Questions
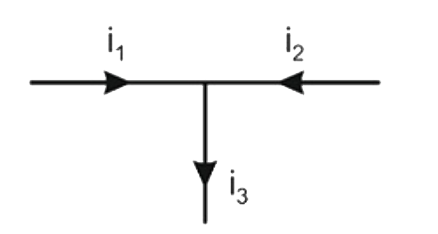
In the given figure, if i1=3sinωtandi2=4cosωt, then i3 is
View SolutionIf two waves represented by y1=4sinωt and y2=3sin(ωt+π3) interfere at a point find out the amplitude of the resulting wave
View SolutionIf a waveform has the equation y1=A1sin(ωt−kx) & y2=A2cos(ωt−kx) , find the equation of the resulting wave on superposition.
View SolutionIf the two waves represented dy y1=4cosωt and y2=3cos(ωt+π/3) interfere at a point, then the amplitude of the resulting wave will be about
View SolutionIf interference is complete or cent percent then the frequency of observed crossover will be
View SolutionTwo waves are given by y1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is -
View Solutionx1=5sin(ωt+30∘)
x2=10cos(ωt)
Find amplitude of resultant SHM.
View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View SolutionTwo simple harmonic motions are given by y1=5sin(ωt−π/3).y2=5(sinωt+√3cosωt). Ratio of their amplitudes is
View Solution