Show that if two inductors with equal inductance L are connected in parallel then the equivalent inductance of combination is L/2.The inductors are separated by a large distance.
The correct Answer is:A, B
To show that if two inductors with equal inductance L are connected in parallel, the equivalent inductance of the combination is L2, we can follow these steps:
1. Understand the Configuration: We have two inductors, both with inductance L, connected in parallel.
2. Formula for Equivalent Inductance in Parallel: The formula for the equivalent inductance Leq of two inductors in parallel is given by:
1Leq=1L1+1L2
where L1 and L2 are the inductances of the individual inductors.
3. Substituting Values: Since both inductors have the same inductance L, we can substitute L1=L and L2=L into the formula:
1Leq=1L+1L
4. Simplifying the Equation: This simplifies to:
1Leq=2L
5. Finding the Equivalent Inductance: To find Leq, we take the reciprocal of both sides:
Leq=L2
6. Conclusion: Therefore, the equivalent inductance of the two inductors connected in parallel is:
Leq=L2
Final Result:
The equivalent inductance of two inductors with equal inductance L connected in parallel is L2.
---
1Leq=1L1+1L2
where L1 and L2 are the inductances of the individual inductors.
1Leq=1L+1L
1Leq=2L
Leq=L2
Leq=L2
The equivalent inductance of two inductors with equal inductance L connected in parallel is L2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-1 PART 2
Explore 51 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-2 PART 1
Explore 14 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Problem
Explore 12 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:HLP
Explore 40 Videos
Similar Questions
Knowledge Check
Two inductors of inductance L each are connected in series with opposite magnetic fluxes. The resultant inductance is
(Ignore mutual inductance)AzeroBLC2LD3LTwo inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
The ratio of current i1/i2 is?
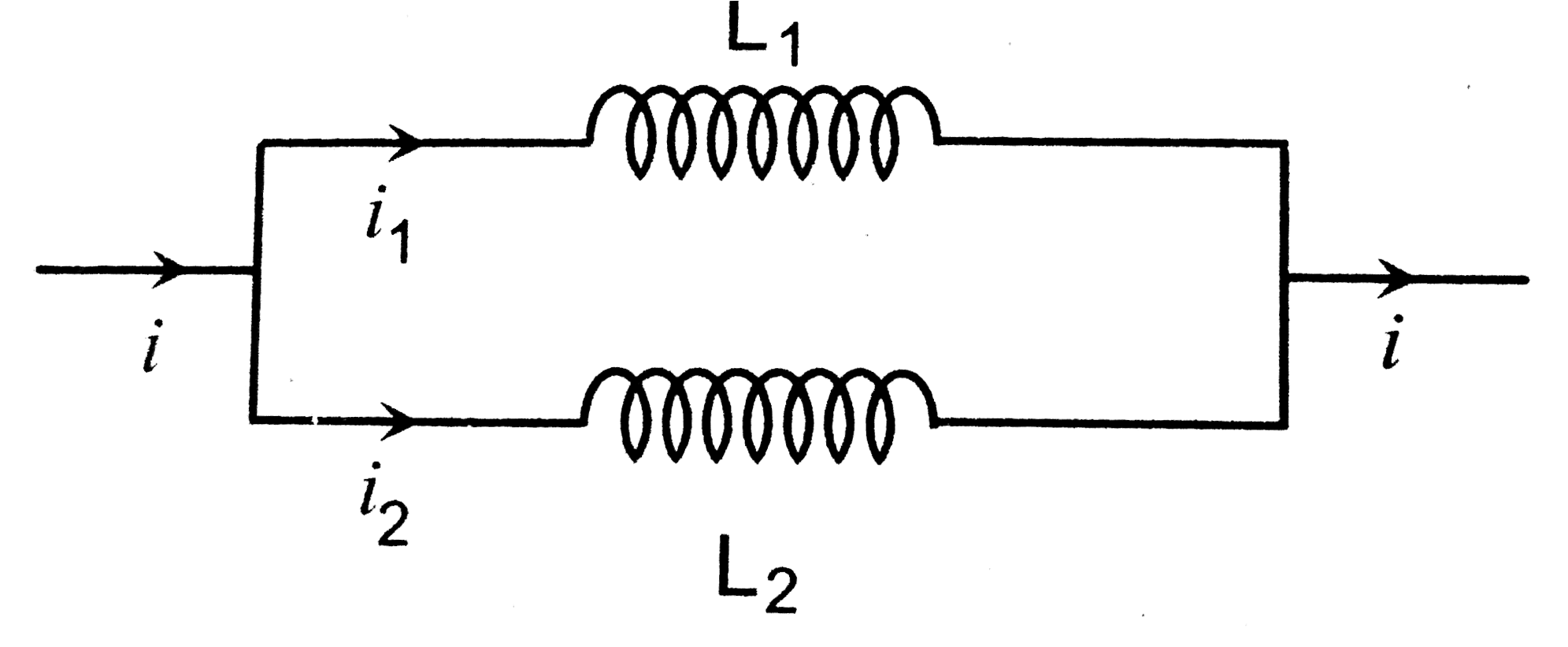 AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2
AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2The equivalent inductance of two inductances is 2.4 henry when connected in parallel and 10 henry when connected in series. The difference between the two inductance is
A8 H, 2HB6H, 4HC5H, 5HD7H, 3H
The inductors of self inductance L1 and L2 are put in series .
View SolutionTwo non-interacting inductor L1 = 2 mH and L2 = 5 mH are connected in parallel then respective ratio of
View SolutionTwo inductors each of inductance L are connected in parallel. One more inductor of value 5 mH is connected in series of this configuration then the effective inductance is 15 mH . The value of L is ………..mH.
View SolutionAn inductor coil of inductance L is divided into two equal parts and both parts are connected in parallel. The net inductance is :
View SolutionTwo inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2

View Solution
