A metallic metre stick translates in a direction making an angle of 60∘ with its length.The plane of motion is perpendicular to a uniform magnetic field of 0.1T that exists in the space.Find the emf induced between the ends of the rod if the speed of translation is 0.2m/s.
The correct Answer is:A, B, C
To solve the problem, we need to find the electromotive force (emf) induced between the ends of a metallic meter stick that is translating in a magnetic field. We will use the formula for induced emf in a moving conductor in a magnetic field.
1. Identify the given values:
- Magnetic field strength, B=0.1T
- Speed of translation, v=0.2m/s
- Length of the rod, L=1m (since it is a meter stick)
- Angle with the direction of motion, θ=60∘
2. Recall the formula for induced emf:
The induced emf (E) in a rod moving in a magnetic field is given by:
E=B⋅v⋅L⋅sin(θ)
3. Substitute the known values into the formula:
E=0.1T⋅0.2m/s⋅1m⋅sin(60∘)
4. Calculate sin(60∘):
sin(60∘)=√32
5. Substitute sin(60∘) into the equation:
E=0.1⋅0.2⋅1⋅√32
6. Perform the multiplication:
E=0.1⋅0.2⋅√32=0.02⋅√32
7. Calculate the final value:
E=0.02√32=0.01√3V
8. Approximate √3:
√3≈1.732
E≈0.01⋅1.732=0.01732V
Thus, the induced emf between the ends of the rod is approximately:
E≈0.01732V or 1.732×10−2V
Final Answer:
The induced emf is approximately 1.732×10−2V.
- Magnetic field strength, B=0.1T
- Speed of translation, v=0.2m/s
- Length of the rod, L=1m (since it is a meter stick)
- Angle with the direction of motion, θ=60∘
The induced emf (E) in a rod moving in a magnetic field is given by:
E=B⋅v⋅L⋅sin(θ)
E=0.1T⋅0.2m/s⋅1m⋅sin(60∘)
sin(60∘)=√32
E=0.1⋅0.2⋅1⋅√32
E=0.1⋅0.2⋅√32=0.02⋅√32
E=0.02√32=0.01√3V
√3≈1.732
E≈0.01⋅1.732=0.01732V
E≈0.01732V or 1.732×10−2V
The induced emf is approximately 1.732×10−2V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem
12 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20 cm s^(-1).
View SolutionA wire of length 10cm translates in a direction making an angle of 60∘ with its length. The plane of motion is perpendicular ot a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation of 20cms−1.
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View SolutionA metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionA metallic wire PQ of length 1cm moves with a velocity of 2m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2T.Find the emf induced between the ends of the wire.Which end will be positively charged.

View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
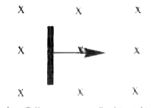
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
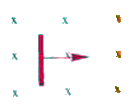
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View Solution
