A charged particle with charge q enters a region of constant, uniform and mutually orthogonal fields →Eand→B with a velocity →v perpendicular toboth →Eand→B, and comes out without any change in its magnitude or direction. Then
→v=→E×→B/B2
→v=→E×→E/B2
→v=→E×→E/E2
→v=→B×→E/E2
The correct Answer is:1
q→v×→B=q→E...(1)
Taking cross product of equation (1) with →B
q(→v×→B)×→B=q(→E×→B)
→v=→E×→B/B2
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-3
29 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-3 PART-1
20 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A charged particle having charge q and mass m is projected into a region of uniform electric field of strength →E0, with velocity →V0 perpendicular to →E0. Throughout the motion apart from electric force particle also experiences a dissipatice force of constant magnitude qE0 and directed opposite to its velocity. If ∣∣→V0∣∣=6m/s, then find its speed when it has turned through an angle of 90∘.
View SolutionA positively charged particle moving due east enters a region of uniform magnetic field directed vertically upwards. The partical will be
View Solution
Knowledge Check
A charged particle with charge q enters a region of constant, uniform and mututally orthogonal fields →Eand→B with a velocity →v perpendicular to both →Eand→B, and comes out without any change in magnitude or direction of →v. Then
A→v=→B×→E/E2B→v=→E×→B/B2C→v=→B×→E/B2D→v=→E×→B/E2
A proton of mass m and charge q enters a region of uniform magnetic field of a magnitude B with a velocity v directed perpendicular to the magnetic field. It moves in a circular path and leaves the magnetic field after completing a quarter of a circle. The time spent by the proton inside the magnetic field is proportional to:
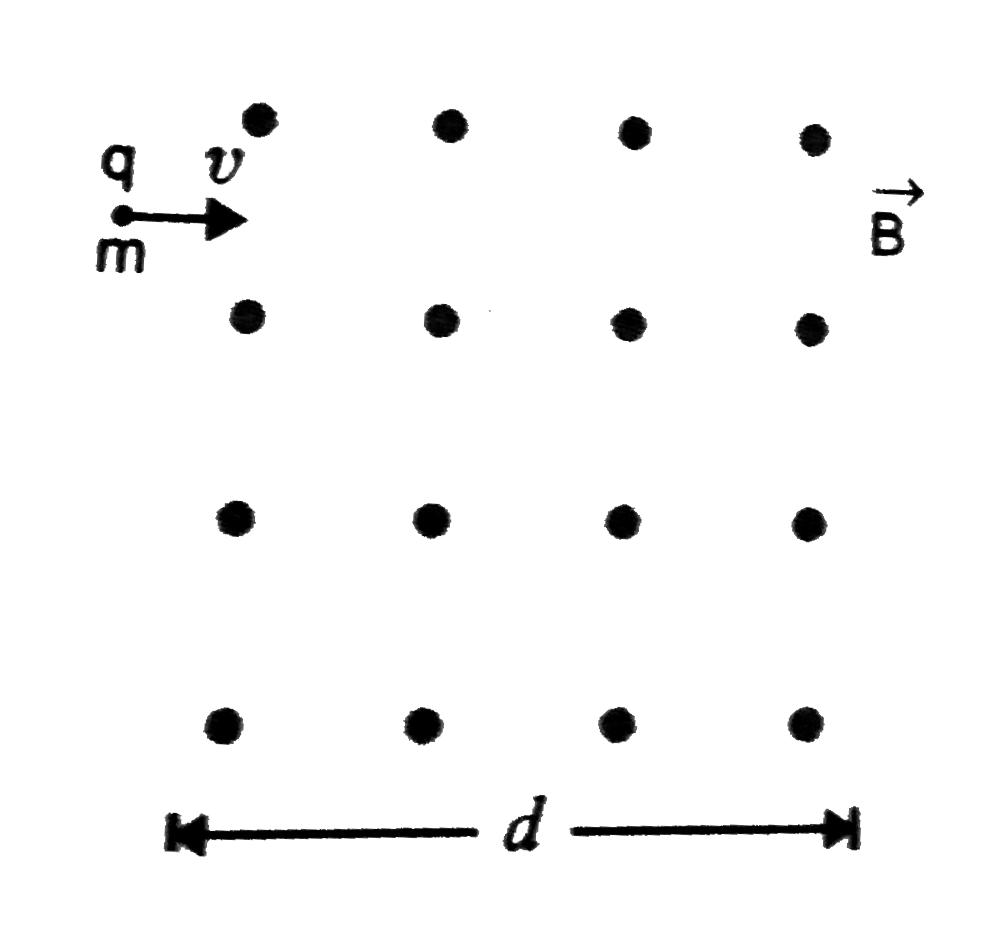
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
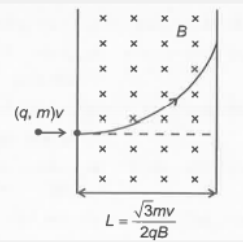
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
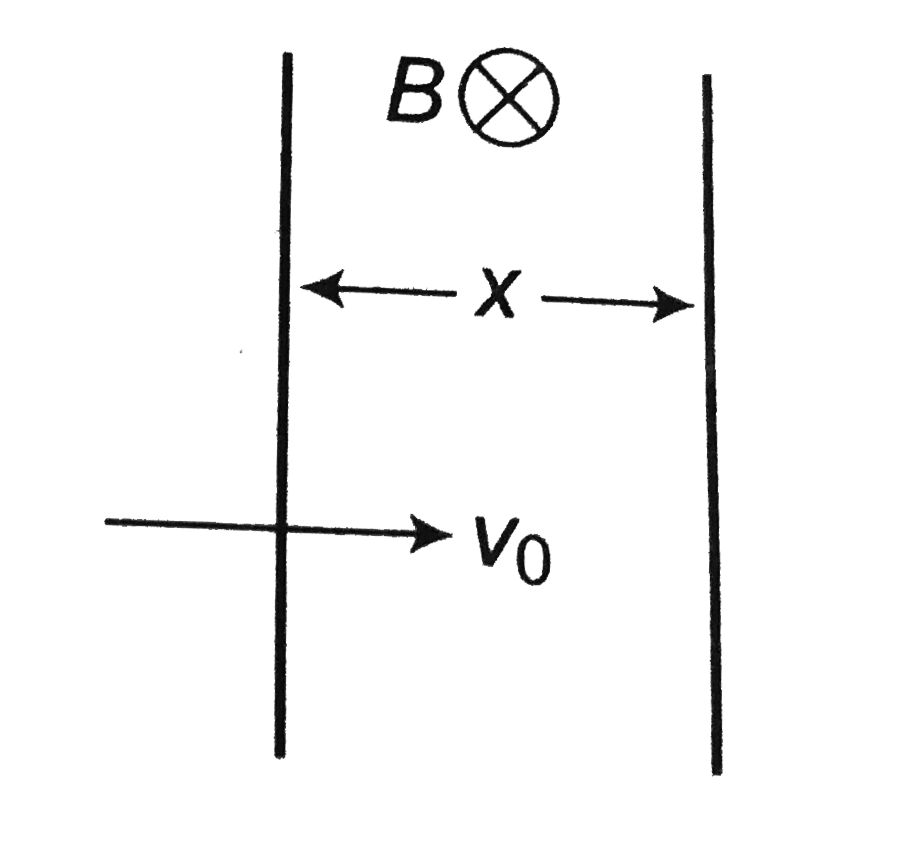
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
View SolutionA proton with velocity →v enters a region of uniform magnetic induction →B, with →v perpendicular to →Band describes a circle of radius R. If an α- particle enters this region with the same velocity →v, it describes a circle of radius
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
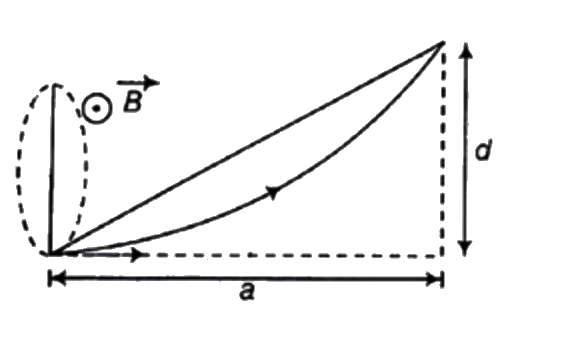
View SolutionA charged particle q enters a region of uniform magnetic field B (out of page) and is deflected distance d after travelling a horizontal distance a. The magnitude of the momentum of the particle is
View Solution
