A converging beam of light rays in incident on a concave spherical mirror whose radius of curvature is 0.8m. Determine the position of the point on the optical axis of the mirror where the reflected rays intersect, if the extensions of the incident rays intersect the optical axis 40cm form the mirror's pole.
The correct Answer is:0.2m,0.5m
To solve the problem step by step, we will use the mirror formula and the information provided in the question.
Step 1: Understand the given data
- Radius of curvature (R) = 0.8 m = 80 cm (since we need to work in centimeters)
- The distance of the incident rays' intersection point from the mirror's pole (u) = 40 cm (this is positive as per the sign convention for object distance)
- The focal length (F) can be calculated using the formula F=R2.
Step 2: Calculate the focal length (F)
Using the formula for focal length:
F=R2=80cm2=40cm
Since the mirror is concave, the focal length is negative:
F=−40cm
Step 3: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length
- v = image distance (what we need to find)
- u = object distance
Step 4: Substitute the known values into the mirror formula
Substituting the values we have:
1−40=1v+140
Step 5: Rearranging the equation
To find 1v, we can rearrange the equation:
1v=1−40−140
Finding a common denominator (which is 40):
1v=−140−140=−240=−120
Step 6: Calculate the image distance (v)
Now, taking the reciprocal to find v:
v=−20cm
Conclusion
The position of the point on the optical axis of the mirror where the reflected rays intersect is at −20cm from the mirror's pole.
- Radius of curvature (R) = 0.8 m = 80 cm (since we need to work in centimeters)
- The distance of the incident rays' intersection point from the mirror's pole (u) = 40 cm (this is positive as per the sign convention for object distance)
- The focal length (F) can be calculated using the formula F=R2.
Using the formula for focal length:
F=R2=80cm2=40cm
Since the mirror is concave, the focal length is negative:
F=−40cm
The mirror formula is given by:
1f=1v+1u
Where:
- f = focal length
- v = image distance (what we need to find)
- u = object distance
Substituting the values we have:
1−40=1v+140
To find 1v, we can rearrange the equation:
1v=1−40−140
Finding a common denominator (which is 40):
1v=−140−140=−240=−120
Now, taking the reciprocal to find v:
v=−20cm
The position of the point on the optical axis of the mirror where the reflected rays intersect is at −20cm from the mirror's pole.
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-2
Explore 62 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
A coverging beam of light is incident on the concave mirror. Then the reflected light :
View SolutionA light ray is incident normally on a plane mirror.
What is its angle of incidence?
View SolutionA light ray is incident normally on a plane mirror.
What is the angle of incidence?
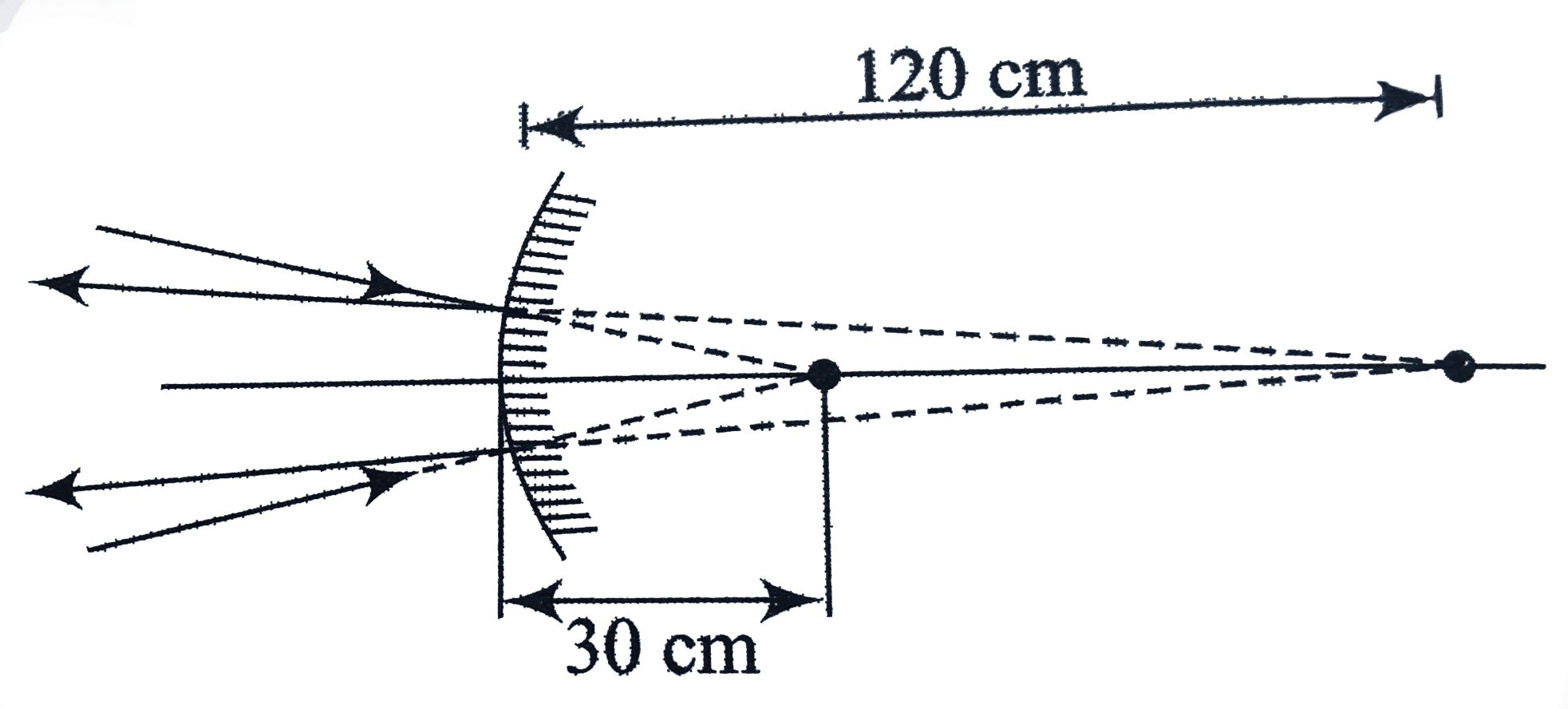
View SolutionConverging rays are incident ono a convex spherical mirror so that their extensions intersect 30cm behind the mirror on the optical axis. The reflected rays form a diverging beam so that their extensions intersect the optical axis 1.2 m from the mirror. Determine the focal length of the mirror.
View SolutionConvex and concave mirrors have the same radii of curvature R. The distanc between the
mirrors is 2R. At what point on the common optical axis of the mirrors should a point source of
light A be placed for the rays to coverage at the point A after being reflected first on the convex
and then on the concave mirror?
View SolutionA convergent beam of light is incident on a convex mirror so as to converge to a distance 12 cm from the pole of the mirror. An inverted image of the same size is formed coincident with the virtual object. What is the focal length of the mirror ?
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘

Find the angle between the mirror and the incident ray.
View Solutiona light ray is incident normally on a plane mirror.
a. What is its angle of incidence?
b. What is the direction of reflected ray? Show it on a diagram.
View SolutionTwo rays are incident on a spherical mirror of radius R = 5 cm parallel to its optical axis at distances h1=0.5cm and h2=3cm Determine the distance Δx between the points at which these rays intersect the optical axis after being reflected at the mirror.
View SolutionThe reflected ray leaves the mirror at not the same angle at which the incident ray strikes it. _____
View Solution

