Convex and concave mirrors have the same radii of curvature R. The distanc between the
mirrors is 2R. At what point on the common optical axis of the mirrors should a point source of
light A be placed for the rays to coverage at the point A after being reflected first on the convex
and then on the concave mirror?
To solve the problem step by step, we need to analyze the situation involving a convex mirror and a concave mirror with the same radius of curvature R and a distance of 2R between them. We will find the position of the point source of light A on the common optical axis so that the rays converge back at point A after reflection from both mirrors.
Step 1: Define the parameters
Let:
- The radius of curvature of both mirrors, R.
- The distance between the mirrors, 2R.
- The position of the point source of light A be at a distance x from the convex mirror.
Step 2: Use the mirror formula for the convex mirror
The mirror formula is given by:
1f=1v+1u
For the convex mirror:
- The focal length f is positive and given by f=R2.
- The object distance u=−x (negative because the object is in front of the mirror).
- The image distance v is what we need to find.
Substituting into the mirror formula:
1R2=1v+1−x
This simplifies to:
2R=1v−1x
Rearranging gives:
1v=2R+1x
Taking the reciprocal, we find:
v=Rx2x+R
Step 3: Determine the object distance for the concave mirror
The image formed by the convex mirror acts as the object for the concave mirror. The distance from the concave mirror to the image formed by the convex mirror is 2R−v.
Using the concave mirror formula:
1f=1v′+1u′
For the concave mirror:
- The focal length f is negative, f=−R2.
- The object distance u′=−(2R−v).
- The image distance v′ is what we need to find.
Substituting into the mirror formula:
−2R=1v′+1−(2R−v)
This simplifies to:
−2R=1v′−1(2R−v)
Rearranging gives:
1v′=−2R+1(2R−v)
Step 4: Set the image distance equal to the object distance
For the rays to converge back at point A, the image distance v′ must equal the object distance x:
x=−2R+1(2R−v)
Step 5: Solve for x
Substituting the expression for v from Step 2 into this equation will allow us to solve for x.
Final Expression
After substituting and simplifying, we will arrive at the value of x which indicates where the point source of light A should be placed.
Conclusion
The position of the point source A can be calculated using the derived equations, and the final answer will provide the exact location on the optical axis.
Let:
- The radius of curvature of both mirrors, R.
- The distance between the mirrors, 2R.
- The position of the point source of light A be at a distance x from the convex mirror.
The mirror formula is given by:
1f=1v+1u
For the convex mirror:
- The focal length f is positive and given by f=R2.
- The object distance u=−x (negative because the object is in front of the mirror).
- The image distance v is what we need to find.
1R2=1v+1−x
This simplifies to:
2R=1v−1x
Rearranging gives:
1v=2R+1x
Taking the reciprocal, we find:
v=Rx2x+R
The image formed by the convex mirror acts as the object for the concave mirror. The distance from the concave mirror to the image formed by the convex mirror is 2R−v.
1f=1v′+1u′
For the concave mirror:
- The focal length f is negative, f=−R2.
- The object distance u′=−(2R−v).
- The image distance v′ is what we need to find.
−2R=1v′+1−(2R−v)
This simplifies to:
−2R=1v′−1(2R−v)
Rearranging gives:
1v′=−2R+1(2R−v)
For the rays to converge back at point A, the image distance v′ must equal the object distance x:
x=−2R+1(2R−v)
Substituting the expression for v from Step 2 into this equation will allow us to solve for x.
After substituting and simplifying, we will arrive at the value of x which indicates where the point source of light A should be placed.
The position of the point source A can be calculated using the derived equations, and the final answer will provide the exact location on the optical axis.
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Single Correct
16 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Objective
12 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A point source of light is placed in front of a plane mirror.
View SolutionA point source of light S is placed on the major optical axis of the concave mirror at a distance of 60 cm. At what distance from the concave mirror should a flat mirror be placed for the rays to converge again at the point S having been reflected from the concave mirror and then from the flat one? Will the position of the point where the rays meet change if they are first reflected from the flat mirror? The radius of the concave mirror is 80 cm.
View SolutionA point object is kept between a plane mirror and a concave mirror facing each other. The distance between the mirrors is 22.5 cm . The distance between the mirrors is 20 cm. what should be the distance of the object from the concave mirror so that after two successive reflections the final image is formed on the object itself ? (consider first reflection from concave mirror).
View SolutionA converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis ?
View SolutionA converging lens and a diverging mirror are placed at a separation of 20 cm. The focal length of the lens is 30 cm and that of the mirror is 50 cm. Where should a point source be placed between the lens and the miror, so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
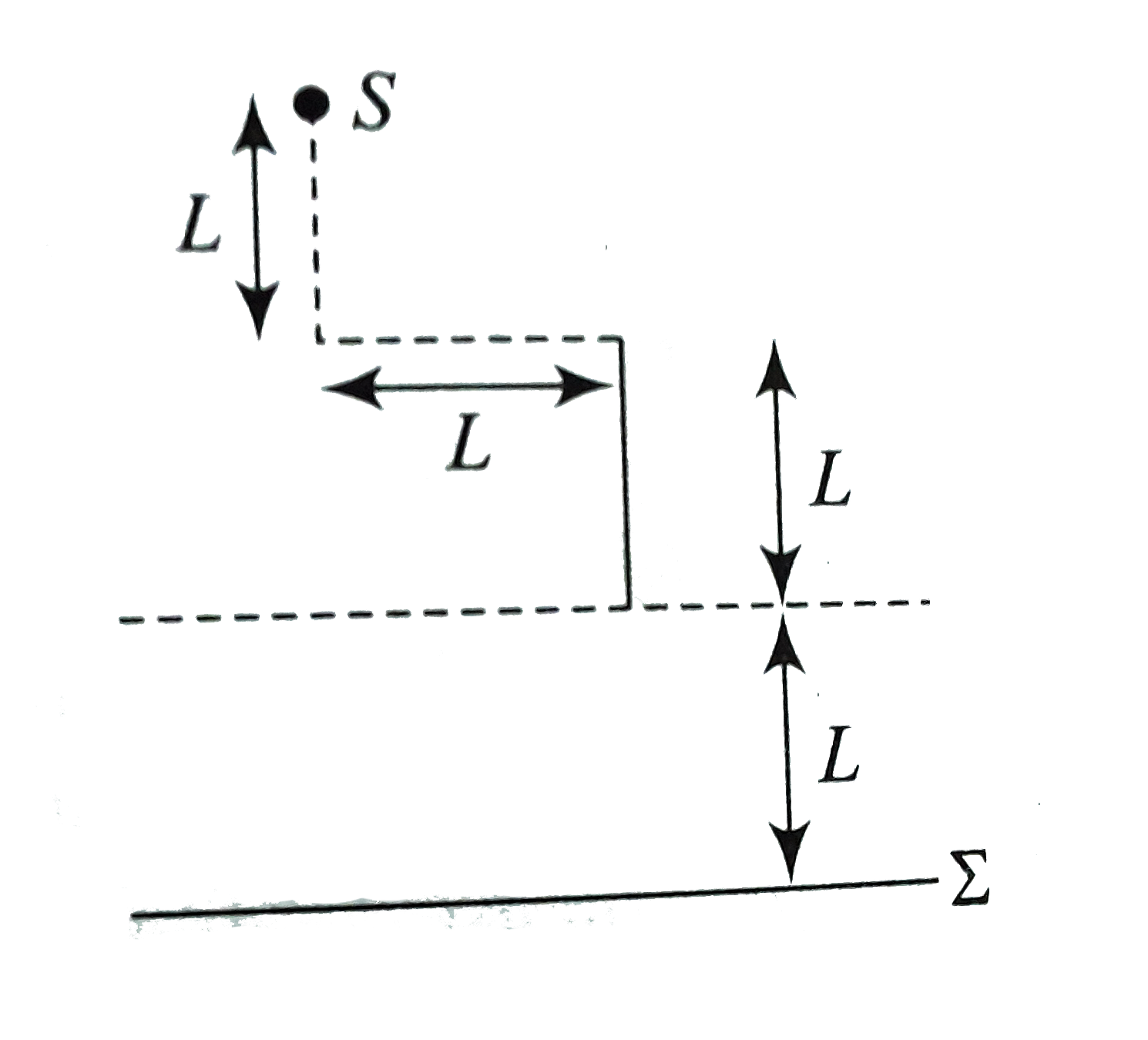
View SolutionA point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
View SolutionA concave mirror of focal length 10cm and a convex mirror of focal length 15cm are placed facing each other 40cm apart. A point object is placed between the mirrors, on their common axis and 15cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
View SolutionTwo spherical mirros (convex and concave) having the same focal length of 36cm are arranged as shwon in figure so that their optical axes coincide. The separation between the mirrors is 1m. At what distance from the concave mirror should an object be placed so that its images formed by the concave and convex mirros independentiy are identical in size

View SolutionA point source is at a distance 35cm on the optical axos from a spherical mirror having a focal length 25cm. At what distance measured along the optical axis form the concave mirror should a plane mirror (perpendicualr to principle axis) be placed for the image it forms (due to rays falling on it after reflection from the concave mirror) to coincide with the point source?
View SolutionA buring candle is placed in front of a concave spherical mirror on its principal optical axis at a distance of (4/3)F form the pole of the mirror (here F is the focal length of the mirror). The candle is arranged at right angle to the axis. The image of the candle in the concave mirror impinges upon a convex mirror of focal length 2F . The distance between the mirrors is 3F and their axes coincide. The image of the candle in the first mirror plays the part of a virtual object with respect to the second mirror and gives a real image arranged between the two mirrors. Find the total linear magnification (magnitude only) of the system.
View Solution
