A biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
Virtual and at a distance of 16cm from mirror
Real and at distance of 16cm from the mirror
Virtual and at a distance of 20cm from the mirror
Real and at a distance of 20cm from the mirror
The correct Answer is:B
First image,
1v−1u=1f
1v−1−30=115
v=30 , iamge in formed 20cm behind the mirror.
Second image, by plane mirror will be at 20cm infront of plane mirror.
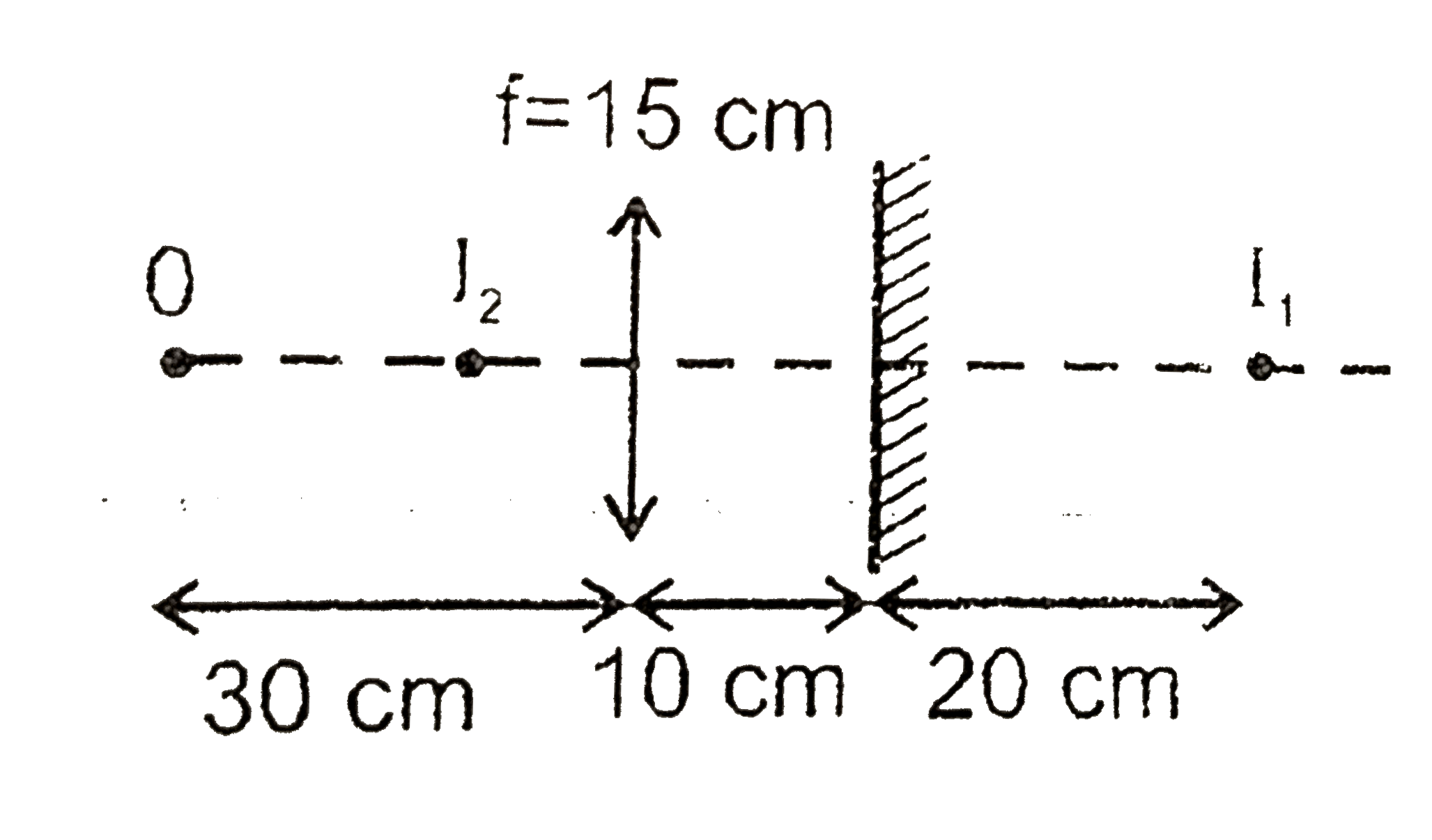
For third image 1v−110=115
1v=110+115=3+230=530
v=6cm
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems
35 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
An optical system consists of two convergent lenses with focal length f1=20cmandf2=10cm. The distance between the lenses is d=30cm. An object is placed at a distance of 30cm from the first lens. At what distance from the second lens will the images be obtained ?
View SolutionA convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png)
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirrorThe size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convax lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cm
A thin convex lens of focal length 'f' is put on a plane mirror as shown in the figure . When an object is kept at a distance 'a' from the lens - mirror combination , its image is formed at a distance a3 in front of the combination . The value of 'a' is :-
_E01_189_Q01.png)
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionA thin bi-convex lens made up of glass of refractive index 3/2 is placed is front of a plane mirror. The space between the lens and the mirror is filled with water of refractive index 4/3 . The radii of curvatures of the lens are R1=15cm and R2=25cm . A point object is placed at distance x from the surface whose curvature is R1. The distance x is greater than the separation between the lens and the mirror. Find the value of x so that image must coincide with the object.
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA converging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed 60 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 50 cm from the lens. Find the locations of the images formed.
View Solution
