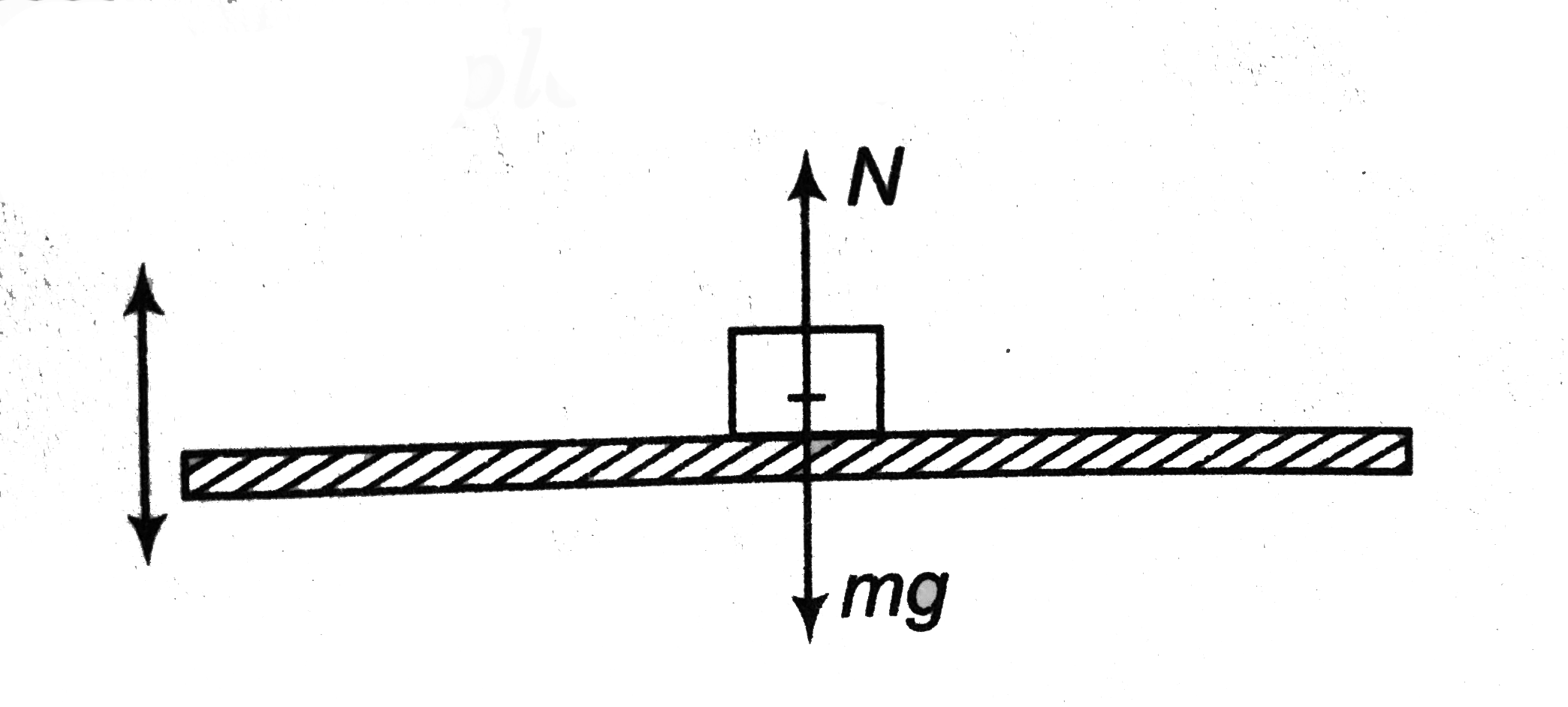
A coin is placed on a horizontal platform which undergoes vertical SHM of angular frequency ω . The amplitude of oscillation is gradually increased. The coin will leave contact with platform for the first time.
at the highest position of the platform
at the mean position of the platform
for an amplitude of gω2
for an amplitude of g2ω2
The correct Answer is:A, C
Aω2=g
⇒A=g/ω2.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - I
20 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
View SolutionA block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
View SolutionA coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
(i) F is always directed towards O
(ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
(iii) F=0 when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
(iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction . The amplitude of oscillation is 2.5 cm what must be the least period of these oscillations so that the object is not detached ?
View SolutionA horizontal platform with an object placed on it is executing S.H.M. in the vertical direction. The amplitude of oscillation is 3.92×10−3m. What must be the least period of these oscillation, so that the object is not detached from the platform
View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction. The amplitude of oscillation is 4×10−3m. The least period of these oscillations, so that the object is not detached from the platform is π5x second. Find value of x. Take g=10m/s2
View SolutionA small coin is placed at a distance r from the centre of a gramophone record.The rotational speed of the record is gradually increased. If the coefficient of friction between the coin and the record is μ, the minimum angular frequency of the record for which the coin will fly off is given by :
View SolutionA particle performing SHM with angular frequency ω=5000 radian/second and amplitude A=2 cm and mass of 1 kg. Find the total energy of oscillation.
View SolutionA horizontal platform with an object placed on it is executing S.H.M. in the vertical direction. The amplitude of oscillation is 3.92×10−3 m. what must ve the least period of these oscillations. So that the object is not detached from the platform
View Solution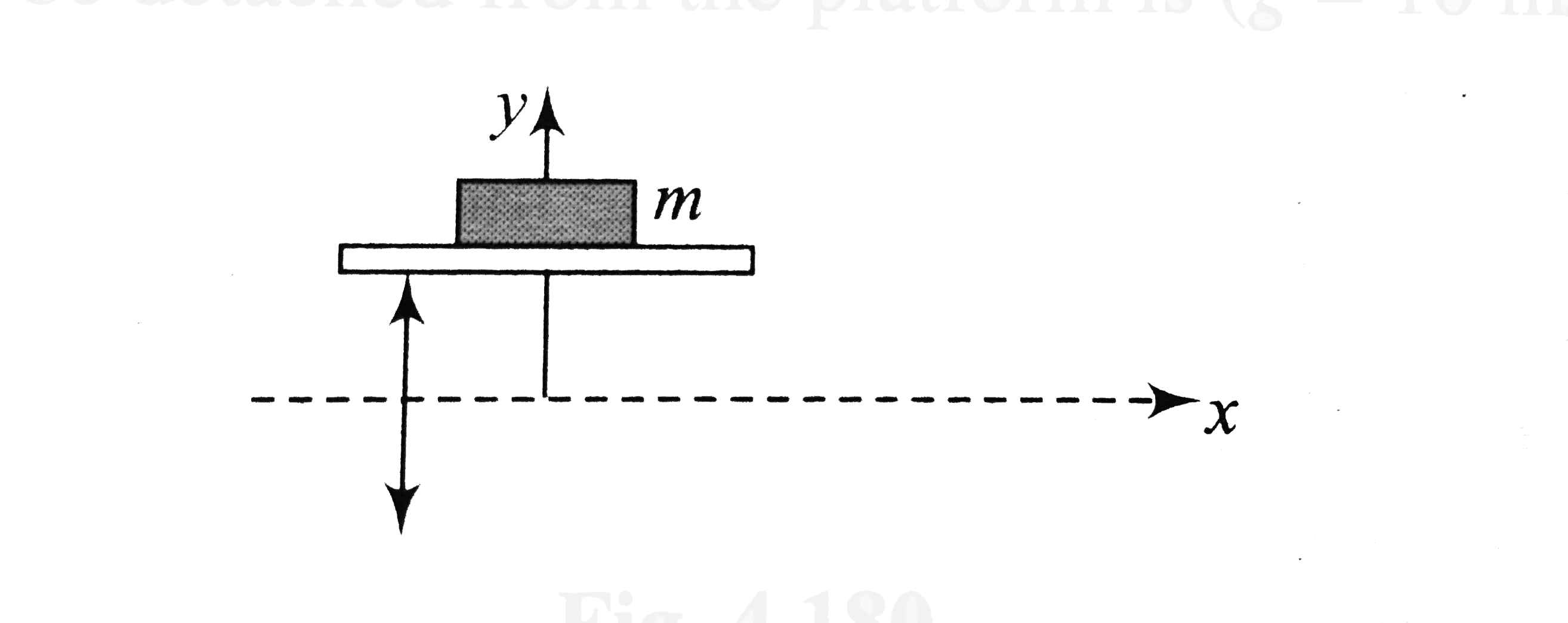
A horizontal platform with a mass m placed on it is executing SHM slong y-axis. If the amplitude of oscillation is 2.5 cm, the minimum period of the motion for the mass not to be detached from the platform (g=10ms2)
View Solution
