An ideal gaseous sample at initial state I is allowed to expand to volume using two different process, in the first process the equation of process is and in second process the equation of the process is .Then
Work done in first process will be greater than work in a second process (magnitude wise)
The order of values of work done can not be compared unless we know the value of and
Values of work done (magnitude) in second process in greater in above expansion irrespective of the value of and
process is not possible
The correct Answer is:C
To solve the problem, we need to analyze the two processes through which the ideal gas expands from an initial state (P0,V0,T0) to a final volume of 2V0. The two processes are defined by the equations PV2=K1 and PV=K2. Let's break down the steps to find the work done in each process.
Step 1: Understand the Processes
1. Process 1: PV2=K1
- This indicates a non-linear relationship between pressure and volume.
2. Process 2: PV=K2
- This indicates an isothermal process (constant temperature) since the product of pressure and volume is constant.
Step 2: Determine the Work Done in Each Process
The work done W in a process can be calculated using the integral:
W=∫VfViPdV
For Process 1: PV2=K1
From the equation, we can express pressure P as:
P=K1V2
Now, substituting this into the work integral:
W1=∫2V0V0K1V2dV
Calculating the integral:
W1=K1(−1V)2V0V0=K1(−12V0+1V0)=K1(12V0)=K12V0
For Process 2: PV=K2
From the equation, we can express pressure P as:
P=K2V
Now, substituting this into the work integral:
W2=∫2V0V0K2VdV
Calculating the integral:
W2=K2(lnV)2V0V0=K2(ln(2V0)−ln(V0))=K2ln(2)
Step 3: Compare the Work Done
Now we have:
- W1=K12V0
- W2=K2ln(2)
To compare W1 and W2, we need to analyze the constants K1 and K2. Without specific values for K1 and K2, we cannot definitively compare the magnitudes of work done in the two processes.
Conclusion
Based on the analysis:
- The work done in the first process cannot be compared to the work done in the second process without knowing the values of K1 and K2.
Thus, the correct answer is:
Option B: The order of value of work done cannot be compared unless we know the value of K1 and K2.
1. Process 1: PV2=K1
- This indicates a non-linear relationship between pressure and volume.
2. Process 2: PV=K2
- This indicates an isothermal process (constant temperature) since the product of pressure and volume is constant.
The work done W in a process can be calculated using the integral:
W=∫VfViPdV
From the equation, we can express pressure P as:
P=K1V2
Now, substituting this into the work integral:
W1=∫2V0V0K1V2dV
Calculating the integral:
W1=K1(−1V)2V0V0=K1(−12V0+1V0)=K1(12V0)=K12V0
From the equation, we can express pressure P as:
P=K2V
Now, substituting this into the work integral:
W2=∫2V0V0K2VdV
Calculating the integral:
W2=K2(lnV)2V0V0=K2(ln(2V0)−ln(V0))=K2ln(2)
Now we have:
- W1=K12V0
- W2=K2ln(2)
Based on the analysis:
- The work done in the first process cannot be compared to the work done in the second process without knowing the values of K1 and K2.
Option B: The order of value of work done cannot be compared unless we know the value of K1 and K2.
Topper's Solved these Questions
Similar Questions
A gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
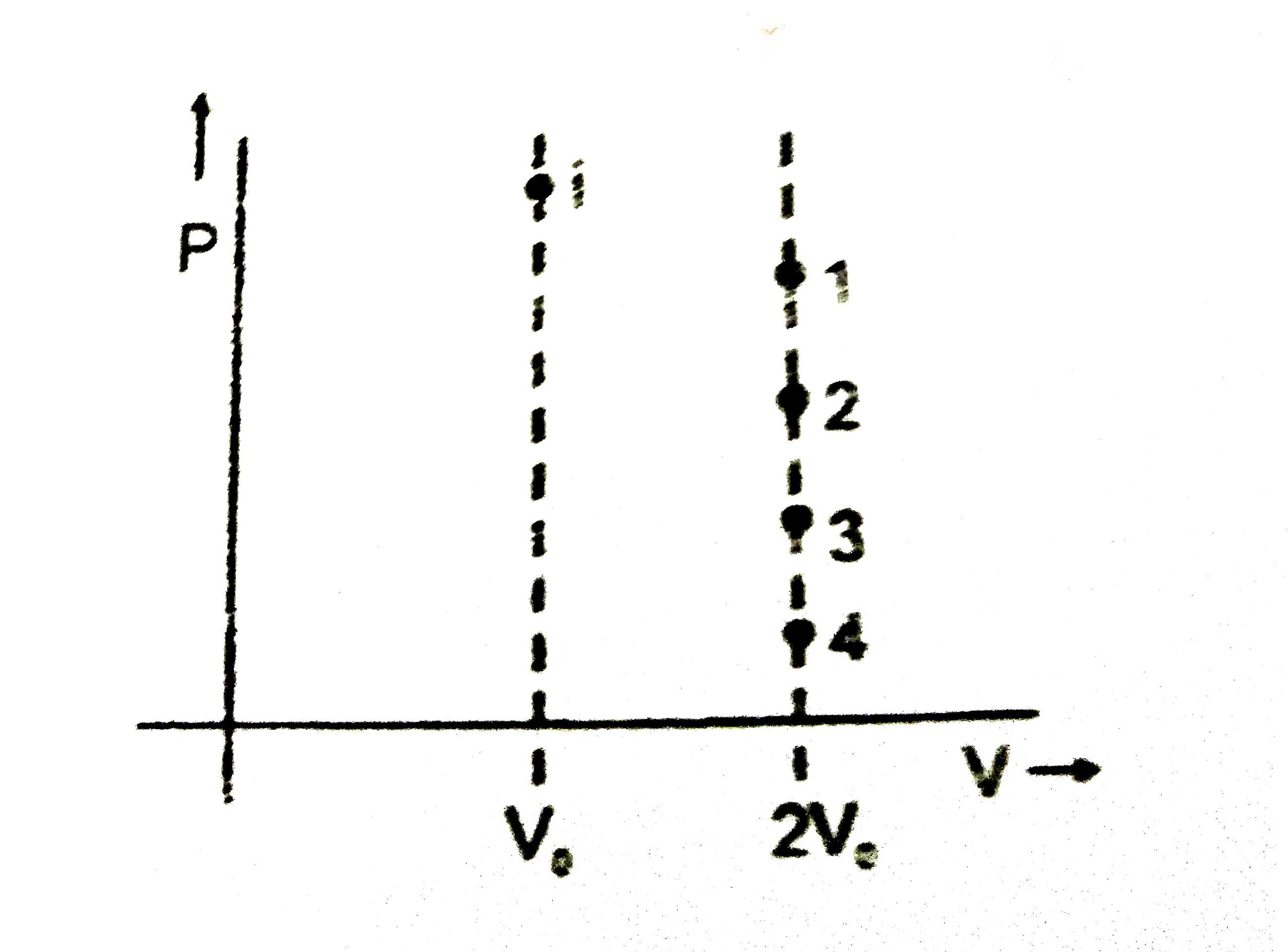
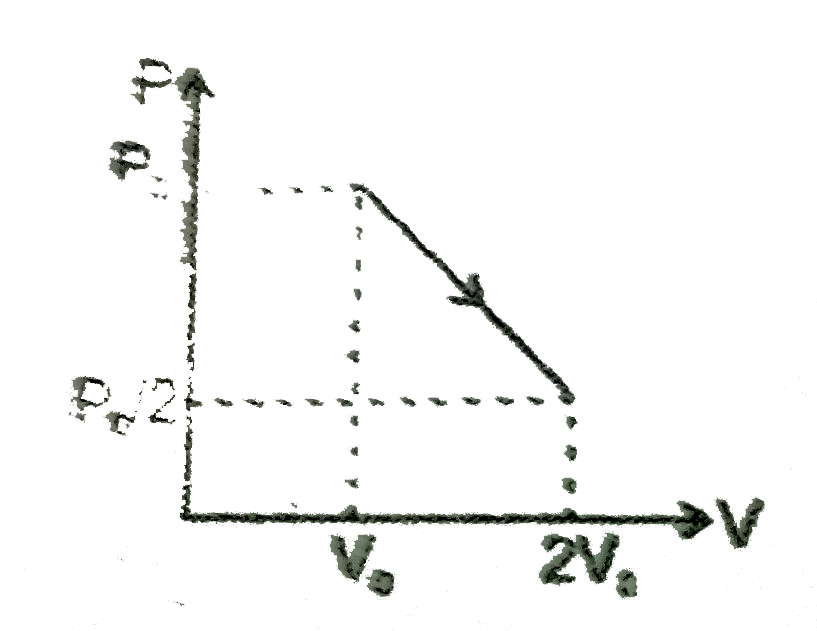
View SolutionAn ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then
View Solution
Knowledge Check
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
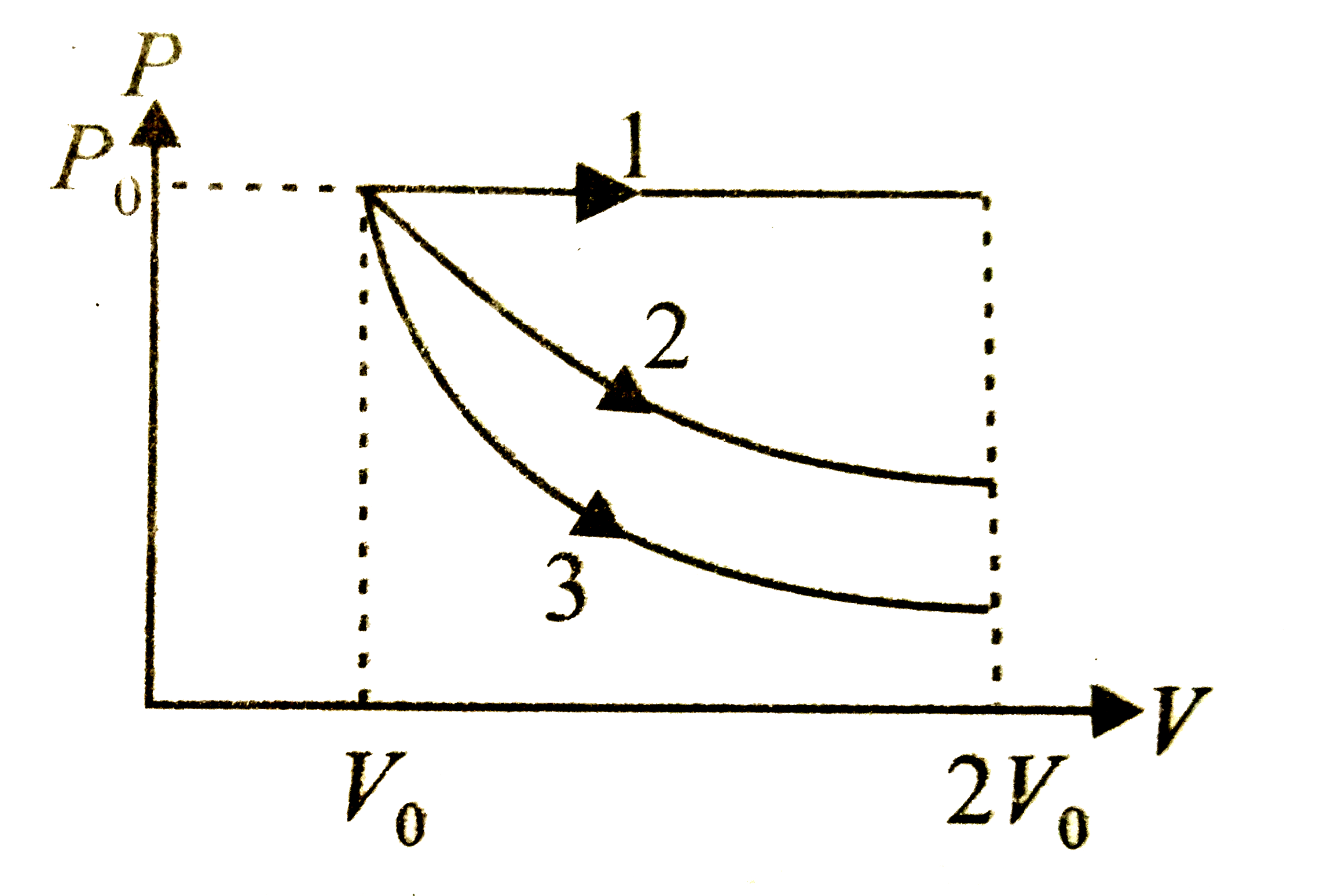 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
An ideal gas can be expanded form an initial state to a certain volume through two different processes PV2= constant and (ii) P=KV2 where K is a positive constant. Then
View SolutionAn ideal gas can be expanded form an initial state to a certain volume through two different processes PV2= constant and (ii) P=KV2 where K is a positive constant. Then
View SolutionAn ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be

View SolutionIn a process V∝T2, temperature of 2 moles of a gas is increased by 200K. Work done by the gas in this process will be
View SolutionThe internal energy of a gas is given by U=2pV. It expands from V0 to 2V0 against a constant pressure p0. The heat absorbed by the gas in the process is
View SolutionThe internal energy of a gas is given by U=2pV. It expands from V0 to 2V0 against a constant pressure p0. The heat absorbed by the gas in the process is
View Solution

