A gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
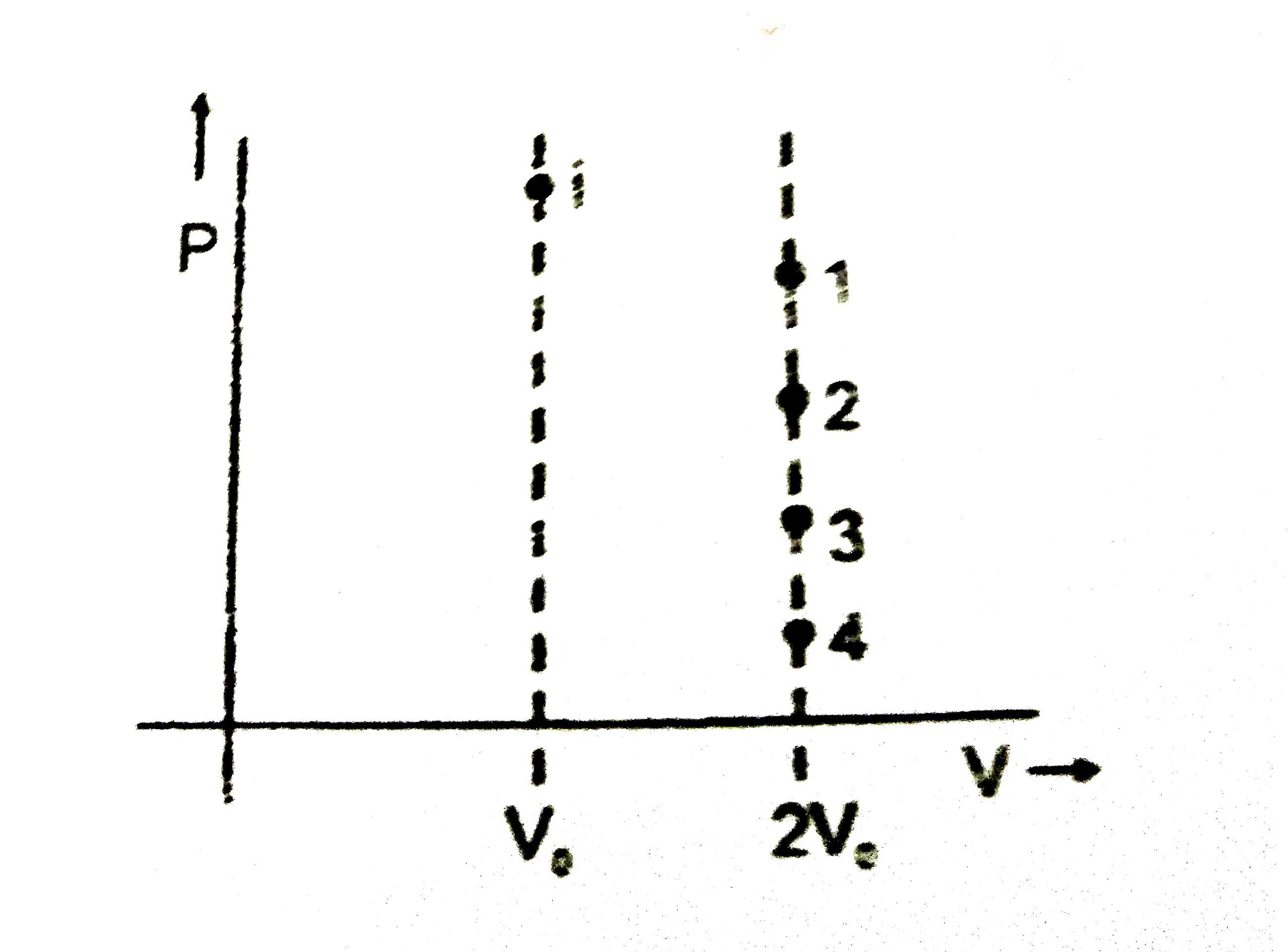
A
1-I, 2-II,3-III,4-IV
B
I-II,2-I,3-IV,4-III
C
2-III,3-II,4-I,1-IV
D
3-II,1-I,3-IV,4-II
Video Solution
Text Solution
The correct Answer is:B
For isothermal irreversible process (T=constant)
P∘V∘=P'2V∘⇒P=P∘2
For P2V=constant
P2oV∘=P22V∘⇒P=P∘√2
Final pressure of isothermal process > Final pressure of adiabatic process. and Final pressure of irreversible adiabatic process > Final pressure of reversible adiabatic process. So, final pressure order II>I>IV>III
|
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-3 Part-1: JEE (ADVANCED)
11 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Main
5 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise 2- III : One or more than one options correct type
14 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Knowledge Check
the work done against force of friction is
A8.7 JB10.7 JC7.8 JD12.7 JThe work done in ergs for the reversible expansion of one mole of an ideal gas from a volume of 10 litres to a volume of 20 litres at 25∘C is
A2.303×298×0.082log102B298×107×8.31×2.303log102C2.303×289×0.082log100.5D2.303×298×2log102.
The work done by 100 calorie of heat in isothermal expansion of ideal gas is :-
View SolutionStatement-1 : Work done in isothermal reversible process is more than irreversible process.
And
Statement-2 : Irreversible process is an infinitesimally slow process.
View SolutionWork done in the isothermal reversible expansion of a gas is always greater than that done in isothermal irreversible expansion of the gas.
View SolutionWork done in reversible isothermal expansion is given by
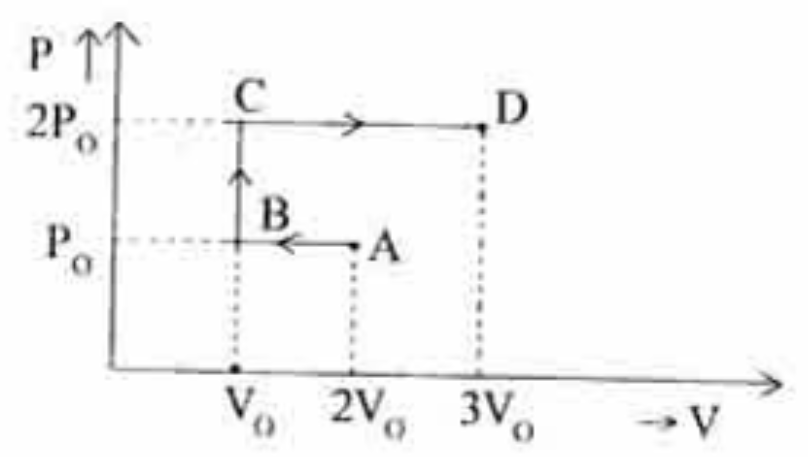
View SolutionThe work done by the gas in the process shown in given P-V diagram is
View SolutionA gas expands by 0.5L against a constant pressure of 1atm. Calculate the work done in joule and calorie.
View Solution