When an atom or an ion is missing from its normal lattice site, a lattice vacancy (Schottky detect) is created In stoichiometric ionic crystals, a vacancy of one ion has to be accompanied by the vacancy of the oppositely charged ion in order to maintain electrical neutrality.
In a Frenkel defect an ion leaves its position in the lattice and occupies an interstitial void.This is the Frenkel defect commonly found along with the Schottky defects and interstitials.In pure alkali halides, Frendel defect are not found since the ions cannot get into the intenstitial sites.Frenkel defects are found in silver halides because of the small size of the ion.Unlike Schottky defects. Frenkel defects do not change the density of the solids.In certain ionic solids (e.g. AgBr) both Schottky and Frenkel defects occur.
The defects discussed above do not disturb the stoichiometry of the crystalline meterial.There is large Such solids showing deviations from the ideal stoichiometric composition form an important group of solids For example in the vanadium oxide, , x can be anywhere between 0.6 and 1.3.There are solids which are difficult to prepare in the stoichiometric composition.Thus, the ideal composition in compounds such as FeO is difficult to obtain (normally we get a composition of but it may range from O to ).Non-stoichiometric behaviour is most commonly found for transition metal compounds through is also known for some lanthanoids and actinodes.
Zinc oxide loses oxygen reversibly at high temperature and turns yellow in colour.The excess metal is accomdated interstitially, giving rise to electrons trapped in the neighbourhood.the enhanced electrical conductivity of the non-stoichiometric ZnO arises from these electrons .
Anion vacancies in alkali halides are produced by heating the alkali halide crystals in an atmosphere of the alkali metal vapour.When the metal atoms deposite on the surface they diffuse into the crystal and after ionisation the alkali metal ion occupies cationic vacancy whereas electron occupies anionic vacancy.Electrons trapped in anion vacancies are referred to as F-centres (from Farbe the German word for colour) that gives rise to interesting colour in alkali halides.Thus, the excess of potassium in KCl makes the crystal appear violet and the excess of lithium in LiCl makes it pink.
In the crystal of , the percentage of Fe (II) will be
The correct Answer is:A
To find the percentage of Fe²⁺ ions in the crystal of Fe₀.93O, we can follow these steps:
Step 1: Understand the Composition
The formula Fe₀.93O indicates that there are 0.93 moles of Fe for every mole of O. In an ideal FeO compound, the ratio of Fe to O is 1:1, meaning that for every Fe²⁺ ion, there is one O²⁻ ion.
Step 2: Calculate Missing Fe²⁺ Ions
Since the formula is Fe₀.93O, we can determine how many Fe²⁺ ions are missing:
- Ideal FeO would have 1 mole of Fe²⁺ for 1 mole of O.
- In Fe₀.93O, the number of Fe²⁺ ions is 0.93.
- Therefore, the number of missing Fe²⁺ ions is:
1−0.93=0.07 moles of Fe²⁺
Step 3: Determine Charge Balance
Each Fe²⁺ ion has a charge of +2. The total positive charge missing due to the absence of 0.07 moles of Fe²⁺ is:
0.07 moles×2 (charge of Fe²⁺)=0.14 positive charge
Step 4: Compensating Charge with Fe³⁺ Ions
To maintain electrical neutrality, the missing positive charge of +0.14 must be compensated by Fe³⁺ ions. Each Fe³⁺ ion has a charge of +3. The number of moles of Fe³⁺ ions required to balance the charge is:
Let x be the moles of Fe³⁺. Then, 3x=0.14⇒x=0.143≈0.04667 moles of Fe³⁺
Step 5: Calculate the Total Moles of Iron
The total moles of iron (Fe) in the crystal is the sum of Fe²⁺ and Fe³⁺ ions:
Total moles of Fe=moles of Fe²⁺+moles of Fe³⁺ = 0.93+0.04667≈0.97667
Step 6: Calculate the Percentage of Fe²⁺
Now, we can calculate the percentage of Fe²⁺ ions in the crystal:
Percentage of Fe²⁺=(0.930.97667)×100≈95.3%
Step 7: Final Calculation for Fe²⁺ Percentage
Since we need the percentage of Fe²⁺ ions, we can also calculate it directly from the total amount:
Percentage of Fe²⁺=100%−Percentage of Fe³⁺
Where the percentage of Fe³⁺ can be calculated as:
Percentage of Fe³⁺=(0.046670.97667)×100≈4.8%
Thus, the percentage of Fe²⁺ would be:
100%−4.8%≈95.2%
Conclusion
The percentage of Fe²⁺ in the crystal of Fe₀.93O is approximately 95.2%.
---
The formula Fe₀.93O indicates that there are 0.93 moles of Fe for every mole of O. In an ideal FeO compound, the ratio of Fe to O is 1:1, meaning that for every Fe²⁺ ion, there is one O²⁻ ion.
Since the formula is Fe₀.93O, we can determine how many Fe²⁺ ions are missing:
- Ideal FeO would have 1 mole of Fe²⁺ for 1 mole of O.
- In Fe₀.93O, the number of Fe²⁺ ions is 0.93.
- Therefore, the number of missing Fe²⁺ ions is:
1−0.93=0.07 moles of Fe²⁺
Each Fe²⁺ ion has a charge of +2. The total positive charge missing due to the absence of 0.07 moles of Fe²⁺ is:
0.07 moles×2 (charge of Fe²⁺)=0.14 positive charge
To maintain electrical neutrality, the missing positive charge of +0.14 must be compensated by Fe³⁺ ions. Each Fe³⁺ ion has a charge of +3. The number of moles of Fe³⁺ ions required to balance the charge is:
Let x be the moles of Fe³⁺. Then, 3x=0.14⇒x=0.143≈0.04667 moles of Fe³⁺
The total moles of iron (Fe) in the crystal is the sum of Fe²⁺ and Fe³⁺ ions:
Total moles of Fe=moles of Fe²⁺+moles of Fe³⁺ = 0.93+0.04667≈0.97667
Now, we can calculate the percentage of Fe²⁺ ions in the crystal:
Percentage of Fe²⁺=(0.930.97667)×100≈95.3%
Since we need the percentage of Fe²⁺ ions, we can also calculate it directly from the total amount:
Percentage of Fe²⁺=100%−Percentage of Fe³⁺
Where the percentage of Fe³⁺ can be calculated as:
Percentage of Fe³⁺=(0.046670.97667)×100≈4.8%
Thus, the percentage of Fe²⁺ would be:
100%−4.8%≈95.2%
The percentage of Fe²⁺ in the crystal of Fe₀.93O is approximately 95.2%.
Topper's Solved these Questions
Similar Questions
A red solide is insoluble in water. However it becomes soluble if some KI is added to water. On heating the red solid in a test tube, there is liberation of some violet coloured fumes and droplets of a metal appear on the cooler parts of the test tube. The red solid is :
02:22View SolutionSodium (Na =23) crystallizen in bcc arrangement with the interfacial separation between the atoms at the edge 53.6pm. The density of sodium crystal is:
01:45View SolutionAssertion: In frekel defect in an ionic crystal, an ion is dispalced from its normal site to an interstitial site. Reason: There is both a vacancy and an intersitial ion.
View SolutionWhich point defect is observed in a crystal when a vacancy is created by an atom or ion missing from its normal position ?
View SolutionAssertion (A) Due to Frenkel defect there is no effect on density of a solid. Reason (R) Ions shift from lattice sites to interstitial sites in Frenkel defect.
View SolutionWhen an atom or an ion is missing from its normal lattice site, a lattice vacancy (Schottky detect) is created In stoichiometric ionic crystals, a vacancy of one ion has to be accompanied by the vacancy of the oppositely charged ion in order to maintain electrical neutrality.
In a Frenkel defect an ion leaves its position in the lattice and occupies an interstitial void.This is the Frenkel defect commonly found along with the Schottky defects and interstitials.In pure alkali halides, Frendel defect are not found since the ions cannot get into the intenstitial sites.Frenkel defects are found in silver halides because of the small size of the Ag+ ion.Unlike Schottky defects. Frenkel defects do not change the density of the solids.In certain ionic solids (e.g. AgBr) both Schottky and Frenkel defects occur.
The defects discussed above do not disturb the stoichiometry of the crystalline meterial.There is large Such solids showing deviations from the ideal stoichiometric composition form an important group of solids For example in the vanadium oxide, VOx, x can be anywhere between 0.6 and 1.3.There are solids which are difficult to prepare in the stoichiometric composition.Thus, the ideal composition in compounds such as FeO is difficult to obtain (normally we get a composition of Fe0.85O but it may range from Fe0.93 O to Fe0.96O).Non-stoichiometric behaviour is most commonly found for transition metal compounds through is also known for some lanthanoids and actinodes.
Zinc oxide loses oxygen reversibly at high temperature and turns yellow in colour.The excess metal is accomdated interstitially, giving rise to electrons trapped in the neighbourhood.the enhanced electrical conductivity of the non-stoichiometric ZnO arises from these electrons .
Anion vacancies in alkali halides are produced by heating the alkali halide crystals in an atmosphere of the alkali metal vapour.When the metal atoms deposite on the surface they diffuse into the crystal and after ionisation the alkali metal ion occupies cationic vacancy whereas electron occupies anionic vacancy.Electrons trapped in anion vacancies are referred to as F-centres (from Farbe the German word for colour) that gives rise to interesting colour in alkali halides.Thus, the excess of potassium in KCl makes the crystal appear violet and the excess of lithium in LiCl makes it pink.
In the crystal of Fe0.93O, the percentage of Fe (II) will be03:42View SolutionWhen an ion leaves its correct lattice site and occupies interstitial sites in its crystal lattice, it is called:
03:20View SolutionAny deviation from the perfectly ordered arrangement constitutes a defect or imperfection. The compounds in which the number of irregularity are present in the arrangement of atoms or ions are called atomic imperfections or point defects. These may be stochiometric or non - stoichlometric. Stoichiometric defects are further classified into Schottky defects in which number of positive and negative ions are missing in equal ratio and Frenkel defects in which an ion leaves its correct lattice sites and occupies on interstitial site. Schottky defect is more common in ionic compounds with high co-ordination number and where the size of positive and negative ions are almost equal, while in Frenkel defects are common in ionic compounds, which have low co-ordination number and in which there is large difference in size between positive and negative ions. In a crystal some ions are missing from normal sites. This is an example of
02:24View SolutionAny deviation from the perfectly ordered arrangement constitutes a defect or imperfection. The compounds in which the number of irregularity are present in the arrangement of atoms or ions are called atomic imperfections or point defects. These may be stochiometric or non - stoichlometric. Stoichiometric defects are further classified into Schottky defects in which number of positive and negative ions are missing in equal ratio and Frenkel defects in which an ion leaves its correct lattice sites and occupies on interstitial site. Schottky defect is more common in ionic compounds with high co-ordination number and where the size of positive and negative ions are almost equal, while in Frenkel defects are common in ionic compounds, which have low co-ordination number and in which there is large difference in size between positive and negative ions. When an ion leaves ir correct lattice and occupies interstital sites in its crystal lattice, it is called
01:29View SolutionThe defect when an ion occupies an interstitial position in the crystal lattice is called
01:02View SolutionIonic lattice has two major point defects, (1) Schottky (2) Frenkel defects, Schottky defects occurs due to the cation - anion pairs missing from the lattice sites, Frenkel defects occur when an ion leaves its lattice site and fits into an interstitial space. The neutrality of the crystals is being maintained and we considered all losses from interstitial postions
Which defect decreases density of the crystal ?01:24View SolutionIonic lattice has two major point defects, (1) Schottky (2) Frenkel defects, Schottky defects occurs due to the cation - anion pairs missing from the lattice sites, Frenkel defects occur when an ion leaves its lattice site and fits into an interstitial space. The neutrality of the crystals is being maintained and we considered all losses from interstitial postions Structure shown here represents
03:53View SolutionIonic lattice has two major point defects, (1) Schottky (2) Frenkel defects, Schottky defects occurs due to the cation - anion pairs missing from the lattice sites, Frenkel defects occur when an ion leaves its lattice site and fits into an interstitial space. The neutrality of the crystals is being maintained and we considered all losses from interstitial postions
Structure shown here represents:
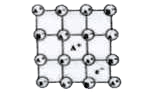 02:26View Solution
02:26View SolutionIonic lattic has two major points defects ,(1) Schottky (2) Frenkel defects . Schottkly defects occurs due to the cations - anion pair's missing from the lattice sites . Frenkel defects occurs when cation leaves its lattice site and fits into an interstitial space. The neutrality of the crystal is being maintained and we considered all losses from interstitial positions.
which defect decrease density of the crystal ?02:07View SolutionIn crystalline solid, atoms, ions or molecules are held in an orderly array. But some point defect is observed in a crystal, when a vacancy is created by an atom or ion dislocated from its normal position to an interstitial site. What is the defect called?
02:11View SolutionA substance 'A' crystallizes in fcc lattice.
In a crystalline solid AB, some vacancy is produced by missing of equal number of oppositely charged ions. What is the defect called?42:40View Solution
