One side of square ABCD is on the line y=2x−17 and other two vertices are on parabola y=x2, if the minimum area of square is A then find A16.
The correct Answer is:5
BC=∣∣2t−t2−17∣∣√5=a
⇒t2−2t+17−√5a=0……..i 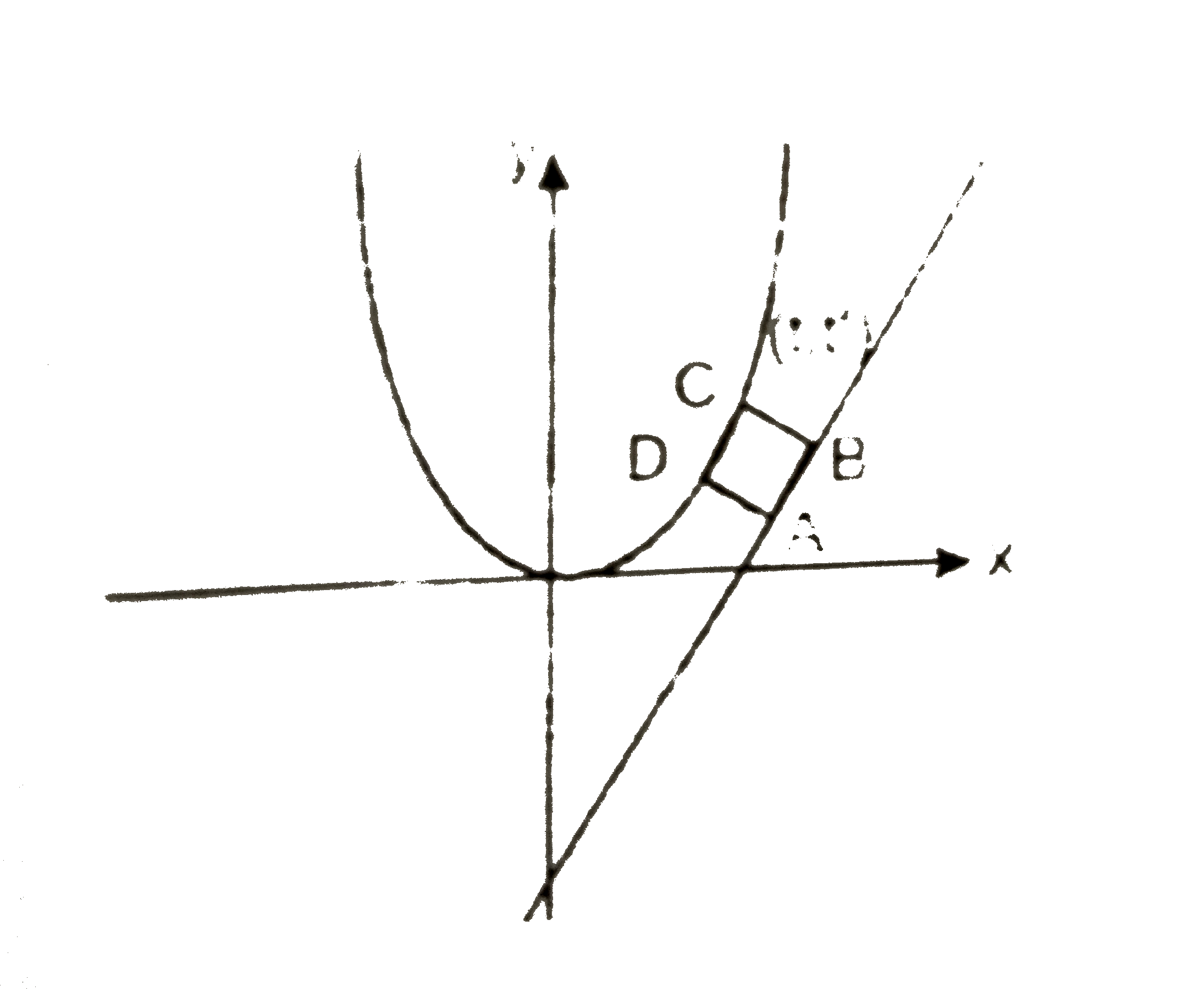
If C(t1,t21),D(t2,t22), then
t1,t2 are roots of equation i and CD=a
⇒t1+t2=2,t1t2=17−√5a
⇒a2=(t1−t2)2+(t21−t22)2
a2=4−4(17−√5a)+4(4−4(17−√5a))
a2=20−20(17)+20√5a
⇒a2=20√5a+320=0
⇒a=16√5 or a=4√5
Minimum area is when a=4√5⇒a2=80
⇒A16=5
Topper's Solved these Questions
Similar Questions
Consider one sides AB of a square ABCD in order on line y=2x−17, and other two vertices C, D on y=x2
The maximum possible area of square ABCD is
View SolutionConsider one sides AB of a square ABCD in order on line y=2x−17, and other two vertices C, D on y=x2
The minimum intercept of line CD on the y-axis is
View Solution
Knowledge Check
If a vertex of a square is at the point (1,−1) and one of its sides lie along the line 3x−4y−17=0, then the area of the square is
A4 sq. unitsB3 sq. unitsC12 sq. unitsD2 sq. units
Two sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionTwo sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionTwo sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionFind the area bounded by the parabola y=x2, the x -axis and the lines x=−1,x=2 .
View SolutionFind the area bounded by the parabola x2=y, x-axis and the line y=1
View Solution

