P is a variable point on the ellipse x22a2+y22b2=1 (a>b) whose foci are F and F'. The maximum area (in unit2)of the ΔPFF' is
2a√a2−b2
2b√a2−b2
a√(2a2−2b2)
b√(2a2−2b2)
The correct Answer is:B
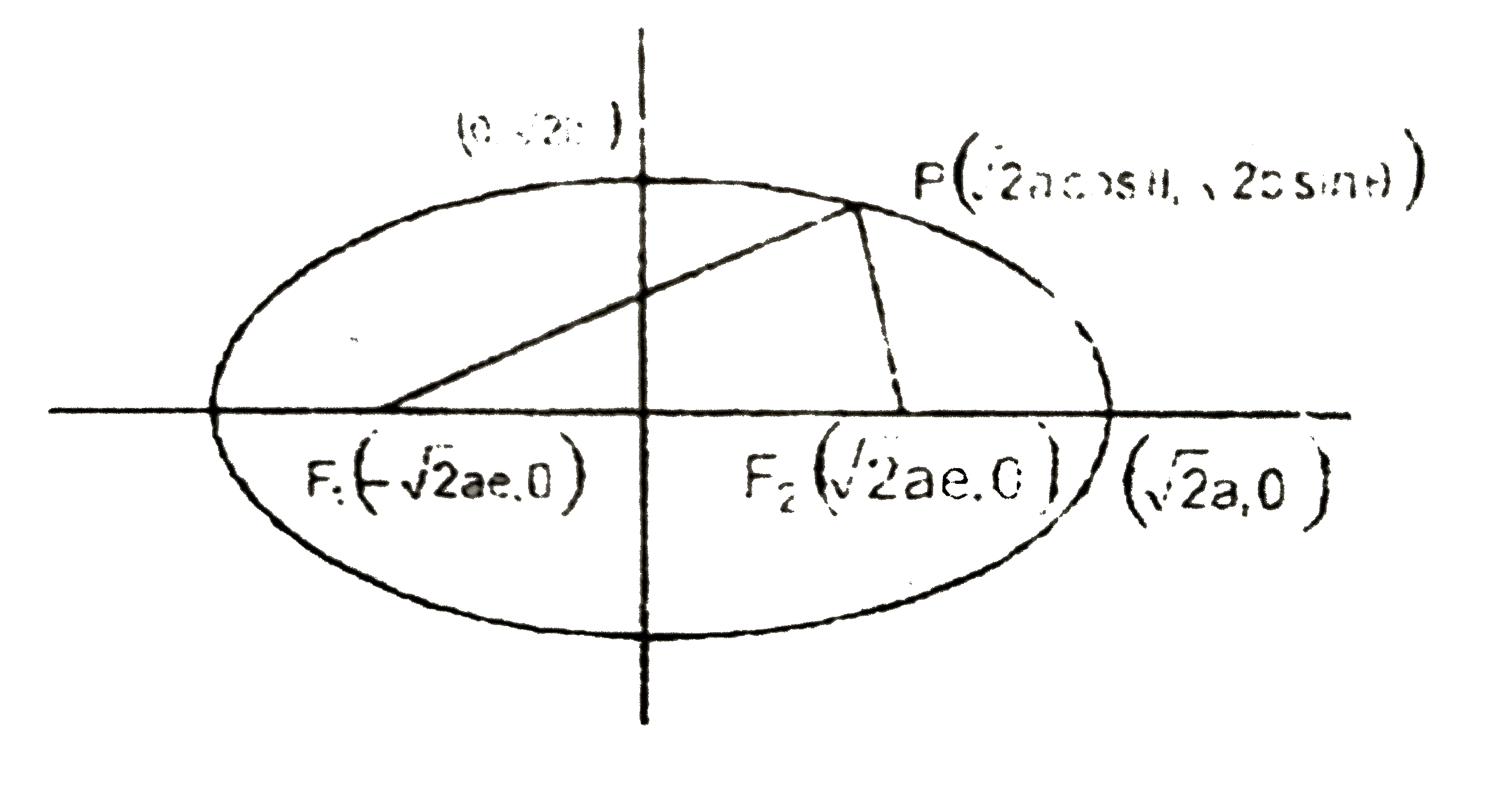
area of ΔPF1F2=A=12(2√2ae)√2bsinθ
⇒A=2abesinθ
=2aba√a2−b2=2b√a2−b2
Topper's Solved these Questions
Similar Questions
P is a variable on the ellipse x2a2+y2b2=1 with ∀' as the major axis. Find the maximum area of triangle APA'
View SolutionThe area of the ellipse x2a2+y2b2=1 is
View SolutionLet P be a variable point on the ellipse x225+y216=1 with foci at S and S'. Then find the maximum area of the triangle SPS'
View SolutionLet P be a variable on the ellipse x225+y216=1 with foci at F1andF2
View SolutionIf P is any point on the ellipse 9x2+36y2=324 whose foci are S and S'. Then, SP + S' P equals
View SolutionIf P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
View SolutionIf P is any point lying on the ellipse x2a2+y2b2=1 , whose foci are SandS'. Let ∠PSS'=αand∠PS'S=β ,then
View SolutionIf e' is the eccentricity of the ellipse x2a2+y2b2=1 (a>b), then
View SolutionIf P is a point on the ellipse X29+y24=1
whose foci are S and S' then the value of PS + PS' is
View SolutionLet P be a variable point on the ellipse x2a2+y2b2=1 with foci F1 and F2. If A is the area of the △PF1F2, then the maximum value of A is
View Solution
