A source is moving across a circle given by the equation x2+y2=R2 with constant speed vS=330π6√3m/s. In clockwise sense. A detector is stationary at the point (2R,0)w.r.t. the centre of the circle. The frequency emitted by the source is fS.
(a) What are the co-ordinates of the source when the detector records the maximum and minimum frequencies. Take speed of sound v=330m/s.
The correct Answer is:(√3R2,R2),(√3R2,−R2)<br>f'min<br>=(6sqrt(3))/(6sqrt(3)+pi)f_(S) , f'_(max) = (6sqrt(3))/(6sqrt(3)-pi)f_(S)
To solve the problem step by step, we need to determine the coordinates of the source when the detector records the maximum and minimum frequencies.
Step 1: Understand the Setup
The source is moving in a circular path defined by the equation x2+y2=R2 with a constant speed vS=330π6√3m/s. The detector is stationary at the point (2R,0) with respect to the center of the circle. The speed of sound is given as v=330m/s.
Step 2: Determine the Conditions for Maximum and Minimum Frequencies
The maximum frequency is recorded when the source is moving directly towards the detector, while the minimum frequency is recorded when the source is moving directly away from the detector.
Step 3: Identify the Positions for Maximum Frequency
The source will be at the maximum frequency when it is at the point on the circle that is closest to the detector. The detector is at (2R,0), and the closest point on the circle will be directly to the left of the detector along the x-axis, which is at the point (R,0).
Step 4: Identify the Positions for Minimum Frequency
The source will be at the minimum frequency when it is at the point on the circle that is farthest from the detector. The farthest point will be directly to the right of the center of the circle, which is at the point (−R,0).
Step 5: Write Down the Coordinates
- The coordinates of the source when the detector records the maximum frequency: (R,0)
- The coordinates of the source when the detector records the minimum frequency: (−R,0)
Summary of the Coordinates
- Maximum Frequency: (R,0)
- Minimum Frequency: (−R,0)
The source is moving in a circular path defined by the equation x2+y2=R2 with a constant speed vS=330π6√3m/s. The detector is stationary at the point (2R,0) with respect to the center of the circle. The speed of sound is given as v=330m/s.
The maximum frequency is recorded when the source is moving directly towards the detector, while the minimum frequency is recorded when the source is moving directly away from the detector.
The source will be at the maximum frequency when it is at the point on the circle that is closest to the detector. The detector is at (2R,0), and the closest point on the circle will be directly to the left of the detector along the x-axis, which is at the point (R,0).
The source will be at the minimum frequency when it is at the point on the circle that is farthest from the detector. The farthest point will be directly to the right of the center of the circle, which is at the point (−R,0).
- The coordinates of the source when the detector records the maximum frequency: (R,0)
- The coordinates of the source when the detector records the minimum frequency: (−R,0)
- Maximum Frequency: (R,0)
- Minimum Frequency: (−R,0)
Topper's Solved these Questions
Similar Questions
A source is moving along a circle X2+Y2=R2 with constant speed Vs=330π6√3m/s in clockwise direction while on observer is stationary at point (2R,0) with respect to the centre of circle frequency emitted by the source is f [velocity of sound V= 330 m/s]

Maximum frequency heard by observer
View SolutionA source is moving along a circle X2+Y2=R2 with constant speed Vs=330π6√3m/s in clockwise direction while on observer is stationary at point (2R,0) with respect to the centre of circle frequency emitted by the source is f [velocity of sound V= 330 m/s]

Maximum wave length received observer
View SolutionWhen the observer moves towards the stationary source with velocity, v1, the apparent frequency of emitted note is f1. When the observer moves away from the source with velocity v1, the apparent frequency is f2. If v is the velocity of sound in air and f1f2 = 2,then vv1 = ?
View SolutionA detector is released from rest over a source of sound of frequency f0=103Hz. The frequency observed by the detector at time t is plotted in the graph. The speed of sound in air is (g=10m/s2)
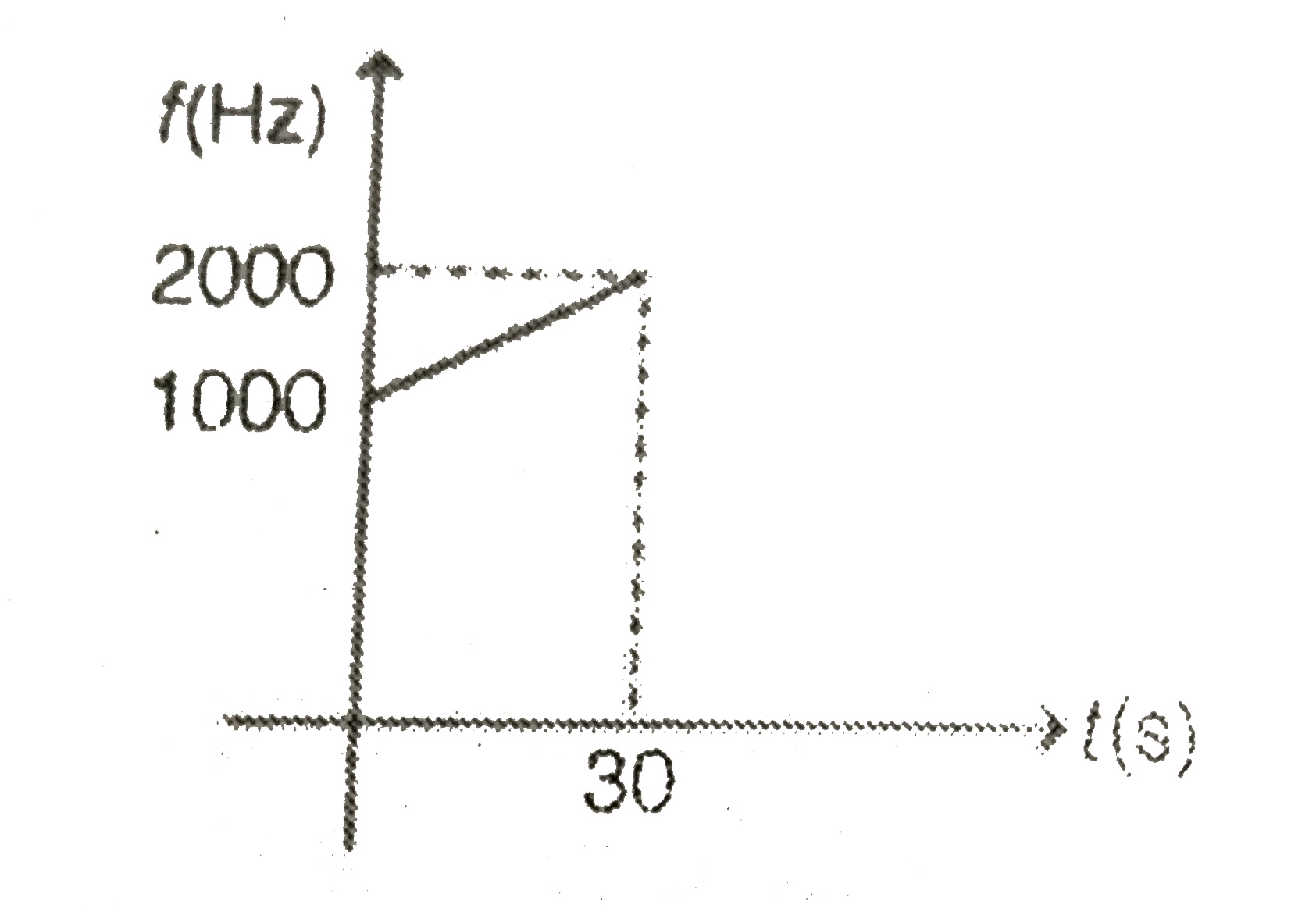
View SolutionA source of sound emitting a frequency 660 Hz is moving counter-clockwise in a circular path of radius 2 metres with an angular velocity 15 rad/s. A recorder at a distance from the source is moving simple harmonically along a straight line with an amplitude 2 metres. The frequency of SHM is 152π per second. The arrangement is shown in figure. When the source is at point A the detector is at D. Find the maximum and minimum frequencies recorded. Velocity of sound in air at this temperature can be taken as 300 m/s

View SolutionA whistle 'S' of frequency v revolves in a circle of radius R at a constant speed v. what is the ratio of the largest and smallest frequency detected by a detector D, at rest, at a distance 2 R from the centre of the circle as shown in the figure? (take speed of sound in air as c)
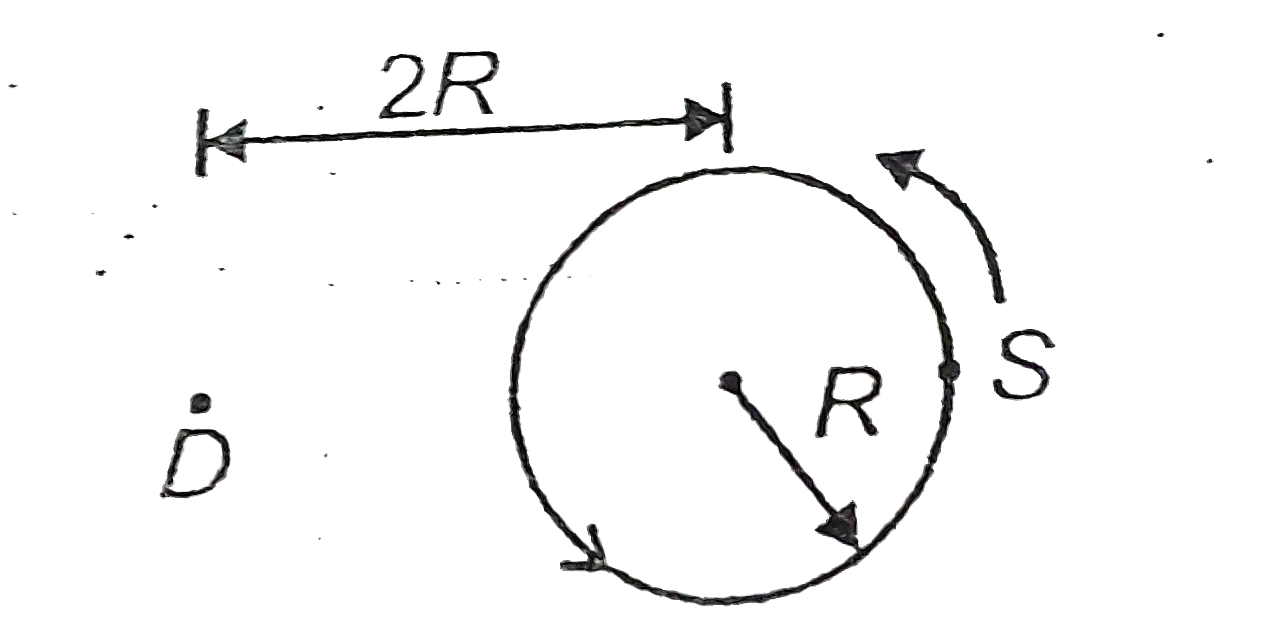
View SolutionA source and a detector move away from each other, each with a speed of 10 m/s with respect to ground with no wind. If the detector detects a frequency 1650 Hz of the sound coming from the source, what is the original frequency of the source? (speed of sound = 340 m/s
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA source and a detector move away from each other, each with a speed of 10ms−1 with respect to the ground with no wind. If the detector detects a frequency 1950 Hz of the sound coming from the source, what is the original frequency of the source? Speed of sound in air =340ms−1.
View SolutionA detector is released from rest over a source of sound of frequency fo=103HZ. The frequency observer by the decector at time t is plotted in the graph. The speed of sound in air (g=10m/s2)
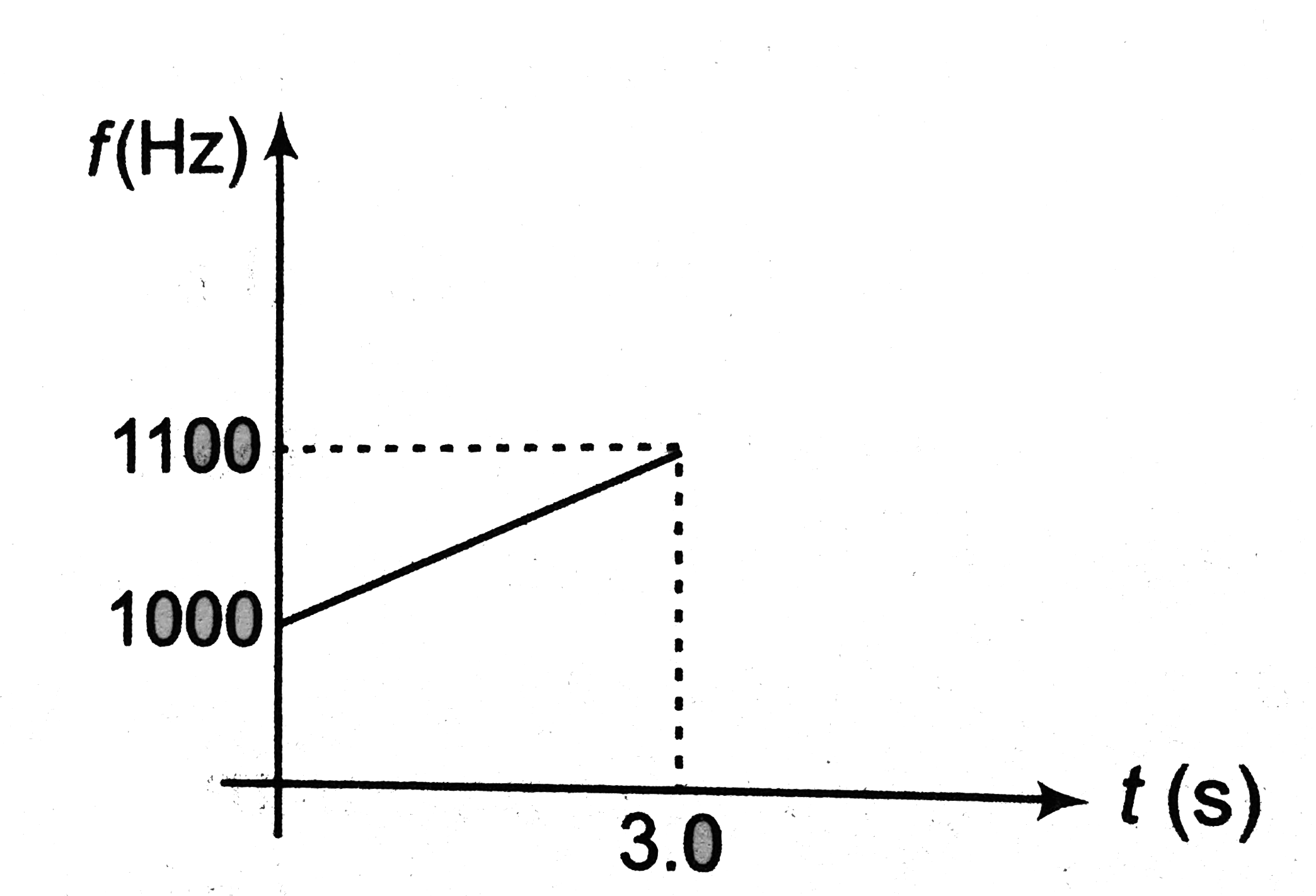
View Solution

