A piece of cork is foating on water in a small tank. The cork oscillates up and doen vertically when small ripples pass over the surface of water. The velocity of the ripples being 0.21ms−1, wavelength 15mm and amplitude 5mm, the maximum velocity of hte piece of cork is

0.44ms−1
0.24ms−1
2.4ms−1
4.4ms−1
The correct Answer is:A
n=Vλ−.2115×10−3=21015
Vmax=Aω=5×10−3×21015×2π
=70×2×227×10−3=.44m/sec.
Topper's Solved these Questions
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I
24 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - II
20 Videos
- SOUND WAVESBOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - I
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise
28 Videos
- STRING WAVESBOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise
32 Videos
Similar Questions
A cork floating on the pond water executes a simple harmonic motion, moving up and down over a range of 4 cm. The time period of the motion is 1 s. at t=0, the cork is at its lowest position of oscillation, the position and velocity of the cork at t=10.5s, would be
View SolutionA cylindrical piece of cork of height 4.9 cm floats in water with its axis vertical and is made to execute slın. Calculate its time period of oscillation if its density is 0.2 gm/cc ?
View Solution
Knowledge Check
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
Fountains usually seen in gardens are generated by a wide pipe with an enclosure at one end having many small holes. Consider one such fountain which is produced by a pipe of internal diameter ? Cm in which water flows at a rate 30ms−1. The enclosure has 100 holes of diameter 0.5cm The velocity of water coming out of the holes is (in ms−1)
View SolutionA small ball is thrown from the edge of one bank of a river of width 100m to just reach the bank. The ball was thrown in the vertical plane (which is also perpendicular to the banks) at an angle 37∘ to the horizonatal. Taking the starting the point as the origin O, verection as positeve y-axis and horizonrtal line passing through the point O and perpenducular to the bank as x-axis find:
(a) Equation of trahectory of the image formed by the water surface
(water surface is at the level y=0)
(b) instantaneous velocity of the image formed due to refraction. [Use g=10m/s2,R.I. of water =4/3]
View SolutionA small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
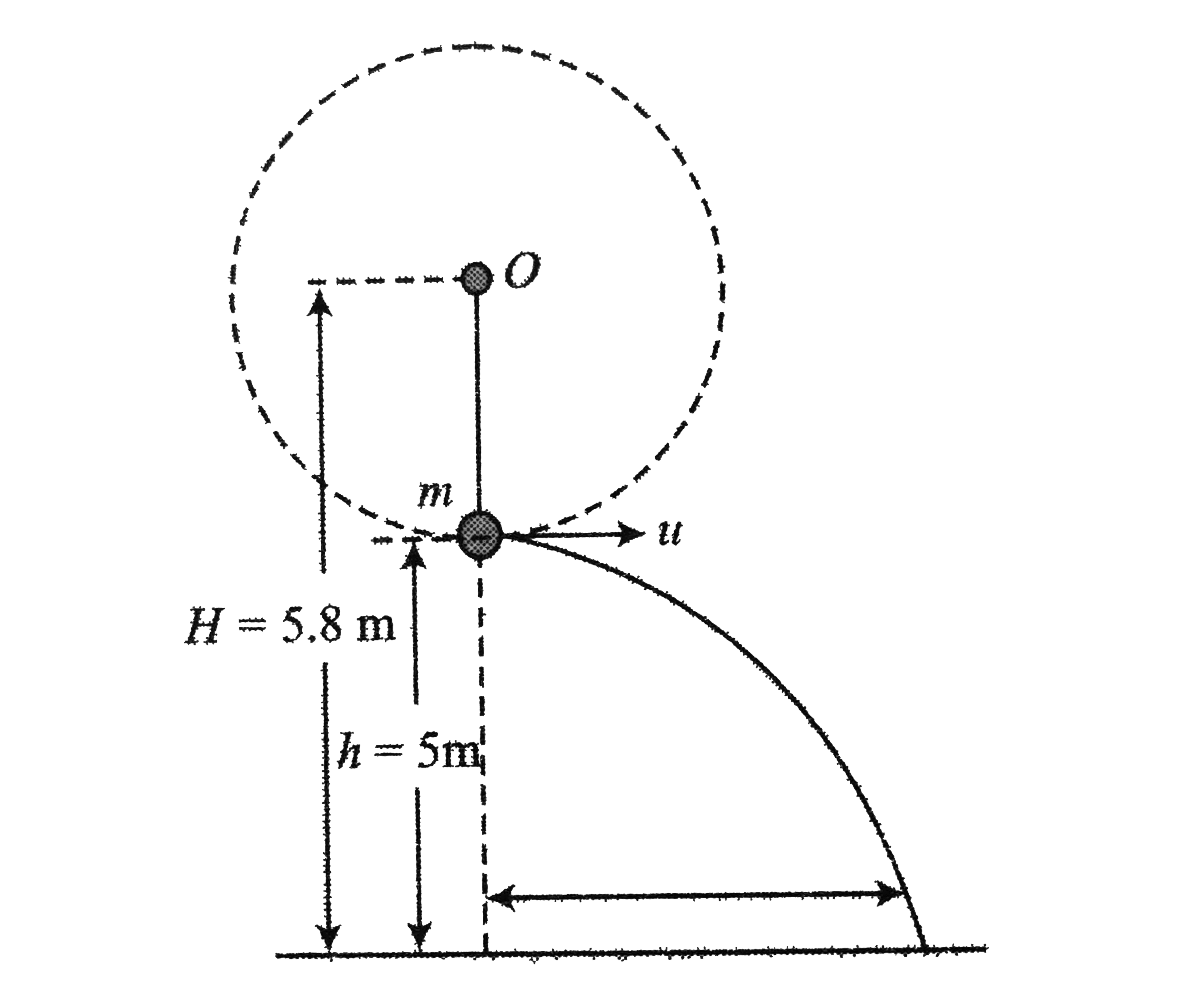
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionAn experimental setup of verification of photoelectric effect is shown in the diagram. The voltage across the electrode is measured with the help of an ideal voltmetar, and which can be varied by moving jockey 'J' on the potentiometer wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2ω. The resistance of 100cm long potentiometer wire is 8ω. The photo current is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photo current in the circuit is very small so we can treat potentiometer circuit an indepdent circuit. The wavelength of various colours is as follows :
_E01_158_Q01.png)
∣∣ ∣∣Light1Violet2Blue3Green4Yellow5Orange6RedλinÅ→4000−45004500−50005000−55005500−60006000−65006500−7000∣∣ ∣∣
When other light falls on the anode plate the ammeter reading remains zero till, jockey till, jockey is moved from the end P to the middle point on the wire PQ. Thereafter the deflection is recorded in the ammeter. The maximum kinetic energy of the emitted electron is :
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the force exerted by water on the curved surface of the conical cork submerged in water when the liquid level in the vessel is equal to H.
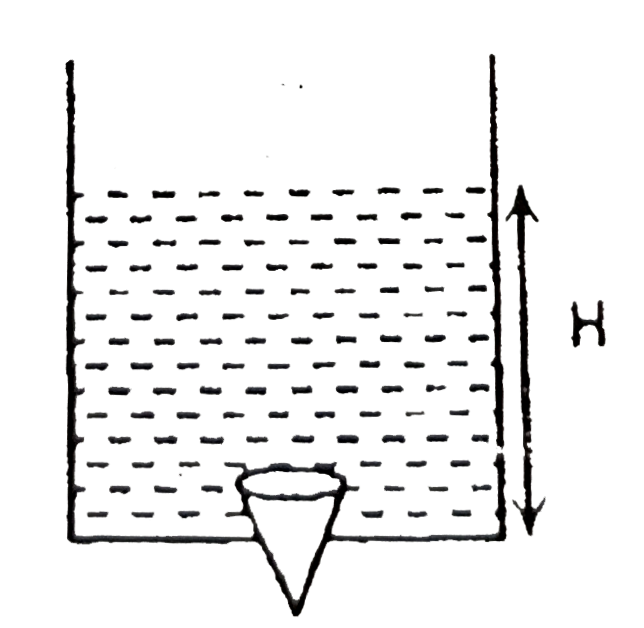
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
The total force exerted by all the fluids on the conical cork in the vertical direction is
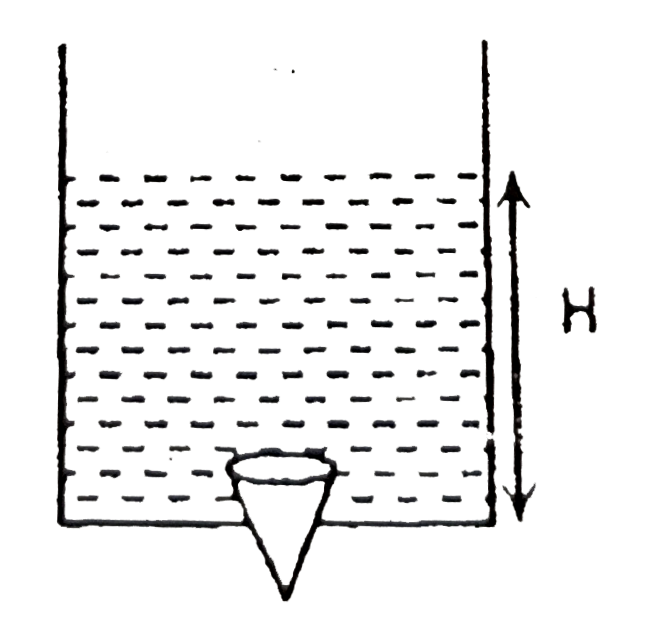
View SolutionA tank has a hole of area 2cm2 at its bottom and in this hole a conical cork is placed and water is filled up. The water level is made to fall slowly by means of another orifice in the tank. When the water level come to a height of 'H'cm, the conical cork just comes out from the hole. Given, volume of water displaced by the cork =80cm3, mass of the cork =40gm, Area of hole =2cm2, density of water =1gm/cm3. Area of circular cross-section of conical cork =8cm2, Height of cork submerged in water =1207cm. Take g=10m/s2, π=227 and P0=105N/m2.
Calculate the value of H.
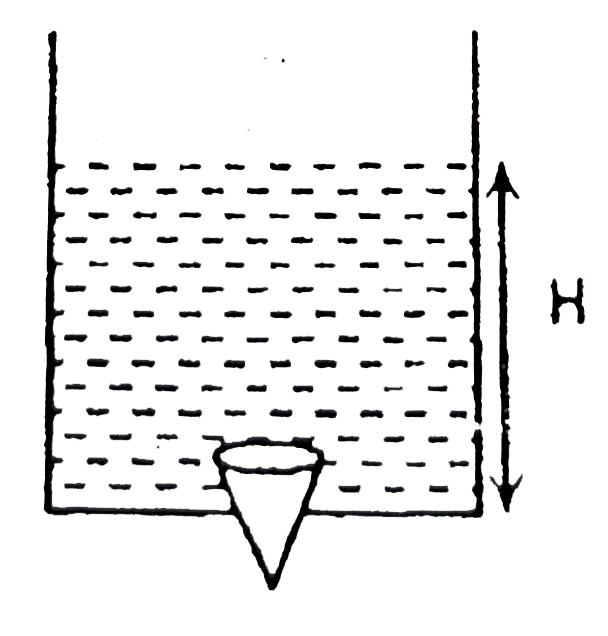
View Solution
