Two rods 'A' & 'B' of equal free length hang vertically 60cm apart and support a rigid bar horizontally. The bar remains horizontal when carrying a load of 5000kg at 20cm from 'A'. If the stress in 'B' is 50N/mm2m, find the stress in 'A' and the areas of 'A' and 'B'
Given YB=9×104N/m2,YA=2×105N/mm2,g=10m/sec2
The correct Answer is:10009N/mm2,300mm2,10003mm2
To solve the problem step by step, we will analyze the forces acting on the rods A and B and apply the principles of equilibrium and stress calculations.
Step 1: Understand the System
We have two rods, A and B, supporting a rigid bar horizontally. The distance between the two rods is 60 cm. A load of 5000 kg is applied at a distance of 20 cm from rod A.
Step 2: Calculate the Weight of the Load
The weight (W) of the load can be calculated using the formula:
W=mg
Where:
- m=5000kg
- g=10m/s2
Calculating the weight:
W=5000×10=50000N
Step 3: Determine the Forces in the Rods
Let FA be the force in rod A and FB be the force in rod B. According to the equilibrium of moments about point A:
FA×20=FB×40
From this, we can express FA in terms of FB:
FA=2FB
Step 4: Relate the Forces to the Total Weight
The total weight supported by both rods is equal to the weight of the load:
FA+FB=50000N
Substituting FA=2FB into the equation:
2FB+FB=50000
3FB=50000
FB=500003≈16666.67N
Now substituting back to find FA:
FA=2FB=2×16666.67≈33333.33N
Step 5: Calculate the Stress in Rod B
Given the stress in rod B is σB=50N/mm2, we can find the area of rod B using the formula:
σB=FBAB
Rearranging gives:
AB=FBσB
Substituting the values:
AB=16666.6750=333.33mm2
Step 6: Calculate the Stress in Rod A
Using Young's modulus for rod B:
YB=σBϵB
Where ϵB is the strain. Since both rods have the same free length and are under the same load conditions, we can relate the stresses and areas using Young's modulus:
σAYA=σBYB
Rearranging gives:
σA=σB×YAYB
Substituting the values:
- YA=2×105N/mm2
- YB=9×104N/mm2
Calculating σA:
σA=50×2×1059×104=50×209≈111.11N/mm2
Step 7: Calculate the Area of Rod A
Using the formula for stress:
σA=FAAA
Rearranging gives:
AA=FAσA
Substituting the values:
AA=33333.33111.11≈300mm2
Final Results
- Stress in rod A: σA≈111.11N/mm2
- Area of rod A: AA≈300mm2
- Area of rod B: AB≈333.33mm2
We have two rods, A and B, supporting a rigid bar horizontally. The distance between the two rods is 60 cm. A load of 5000 kg is applied at a distance of 20 cm from rod A.
The weight (W) of the load can be calculated using the formula:
W=mg
Where:
- m=5000kg
- g=10m/s2
W=5000×10=50000N
Let FA be the force in rod A and FB be the force in rod B. According to the equilibrium of moments about point A:
FA×20=FB×40
From this, we can express FA in terms of FB:
FA=2FB
The total weight supported by both rods is equal to the weight of the load:
FA+FB=50000N
2FB+FB=50000
3FB=50000
FB=500003≈16666.67N
FA=2FB=2×16666.67≈33333.33N
Given the stress in rod B is σB=50N/mm2, we can find the area of rod B using the formula:
σB=FBAB
Rearranging gives:
AB=FBσB
Substituting the values:
AB=16666.6750=333.33mm2
Using Young's modulus for rod B:
YB=σBϵB
Where ϵB is the strain. Since both rods have the same free length and are under the same load conditions, we can relate the stresses and areas using Young's modulus:
σAYA=σBYB
Rearranging gives:
σA=σB×YAYB
Substituting the values:
- YA=2×105N/mm2
- YB=9×104N/mm2
σA=50×2×1059×104=50×209≈111.11N/mm2
Using the formula for stress:
σA=FAAA
Rearranging gives:
AA=FAσA
Substituting the values:
AA=33333.33111.11≈300mm2
- Stress in rod A: σA≈111.11N/mm2
- Area of rod A: AA≈300mm2
- Area of rod B: AB≈333.33mm2
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 3 PART - IV
Explore 9 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 92 illustration
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 43 Videos
Similar Questions
Knowledge Check
A steel cable with a radius 2 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108Nm−2, the maximam load the cable can support
A4π×105NB4π×104NC2π×105ND2π×104
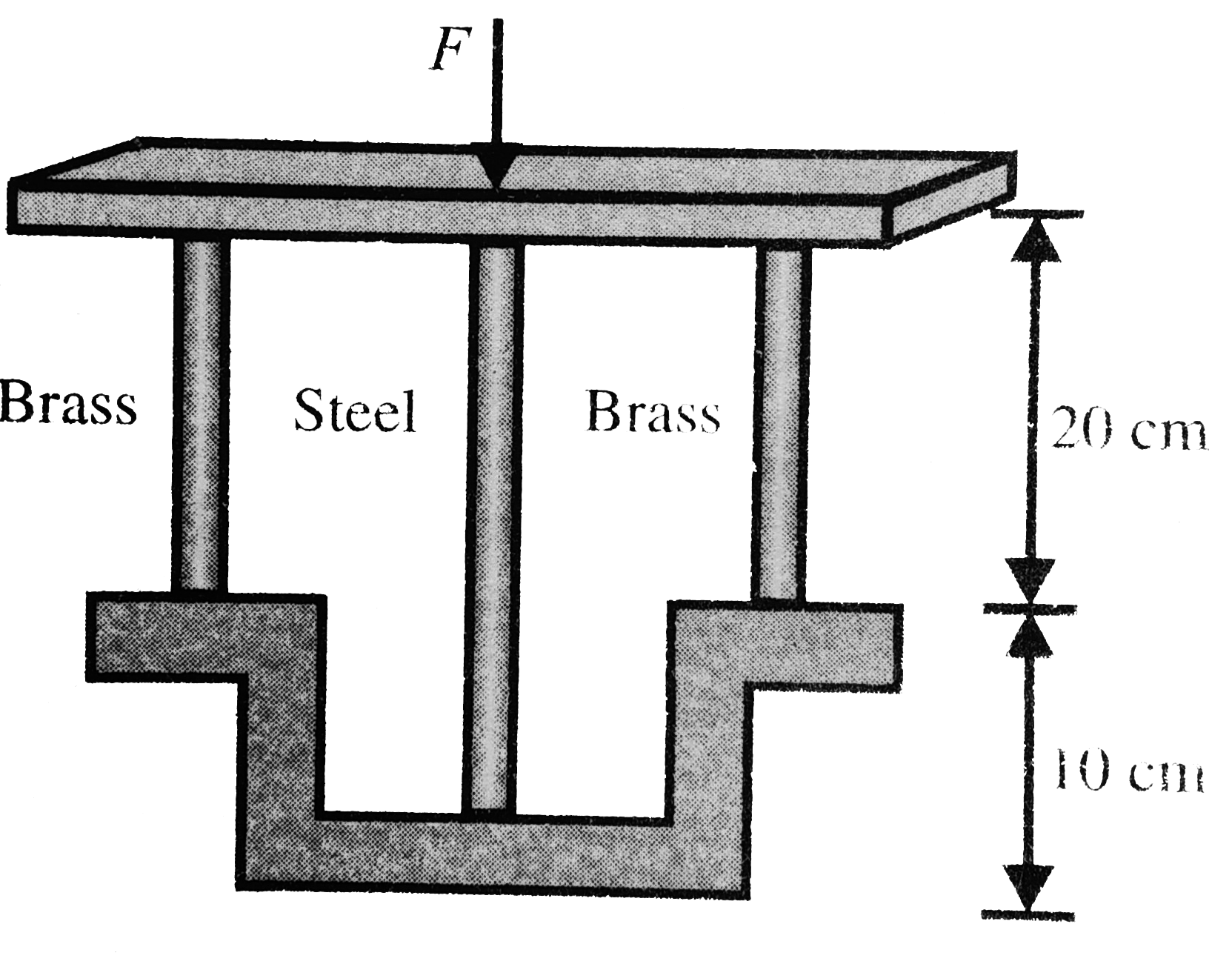
A steel rod of length l1=30cm and two identical brass rod of length l2=20cm each support a light horizontal platform as shown in Fig. Cross-sectional area of each of the three rods is A=1cm2. A vertically downward force F=5000N is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2 and brass Yb=1×1011Nm−2. Find stress (in MPa) developed in a. Steel rod b. Brass rod
View SolutionA block of mass 4 kg is suspended from the ceiling with the help of a steel wire of radius 2mm and negligible mass. Find the stress in the wire. (g=π2) (A) 4.0×106N/m2 (B) 3.14×106N/m2 (C) 3×105N/m2 (D) 2.0×106N/m2
View SolutionA steel wire having a radius of 2.0mm, carrying a load of 4kg, is hanging from a celling. Given that g=3.1πms−2, what will be the tensile stress that would be developed in the wire?
View SolutionWhat will be the stress at −20∘C, if a steel rod with a cross-sectional area of 150 mm2 is stretched between two fixed points? The tensile load at 20∘C is 5000 N (Assume, α=11.7×10−6/∘C and Y = 200×1011N//m^(2))
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
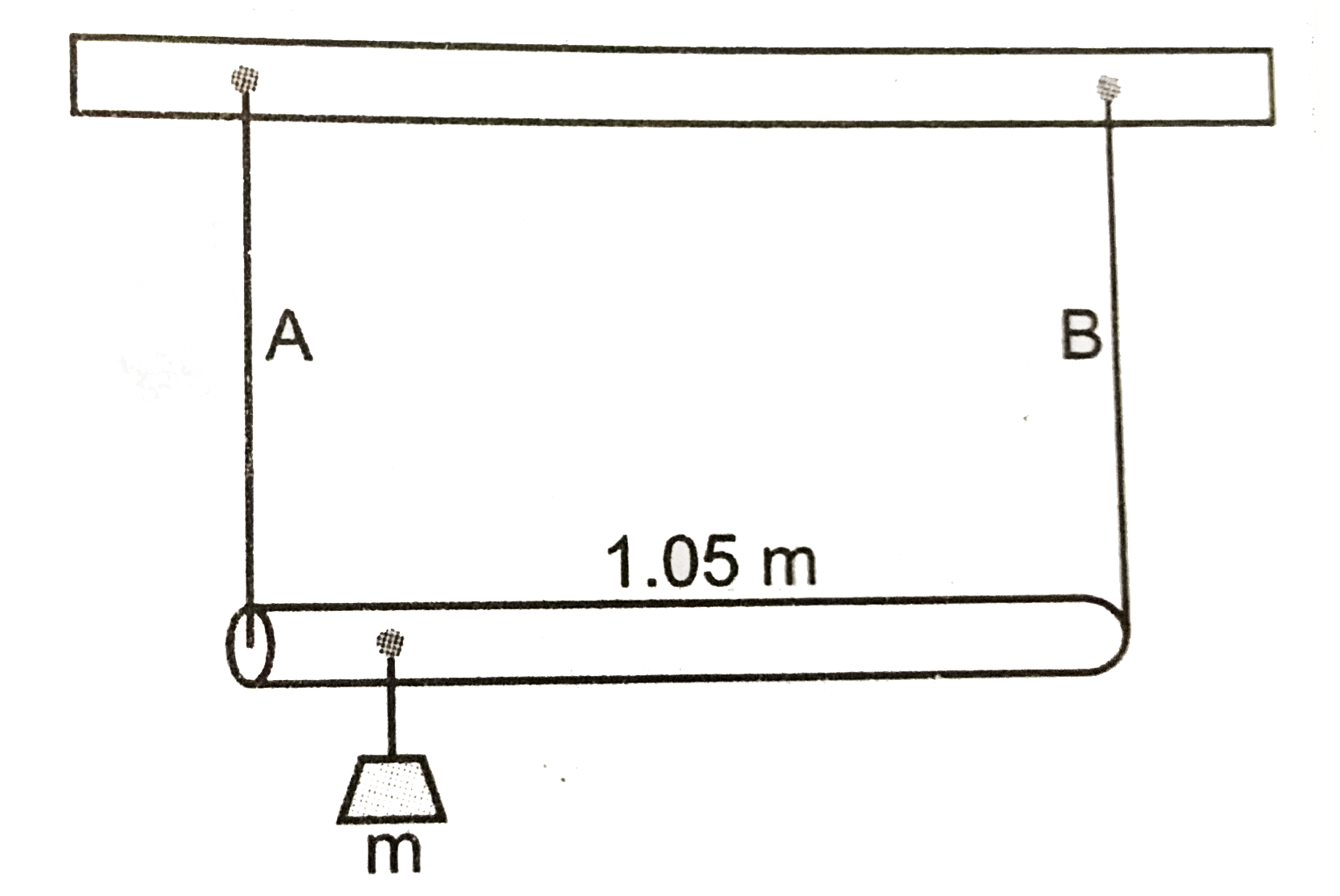
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2

View SolutionA brass of length 2m and cross-sectional area 2.0cm2 is attached end to end to a steel rod of length and cross-sectional area 1.0cm2. The compound rod is subjected to equal and oppsite pulls of magnitude 5×104N at its ends. If the elongations of the two rods are equal, the length of the steel rod (L) is
{YBrass=1.0×1011N/m2 and Ysteel=2.0×1011N/m2
View Solution


