A ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

The correct Answer is:6

mv2+mg(R−r)(1−cosθ)= constant
⇒2mvdvdt+mg(R−r)sinθdthηdt=0
since v=ω(R−r)=−dthηdt(R−r)
dvdt=−d2θdt2(R−r)
2mdthηdt(R−r)d2θdt2(R−r)+mg(R−r)sinθdthηdt=0
⇒d2θdt2=−>hη2(R−r) (for small θ,sinθ=0)
⇒T=2π√2(R−r)g
Similar Questions
A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
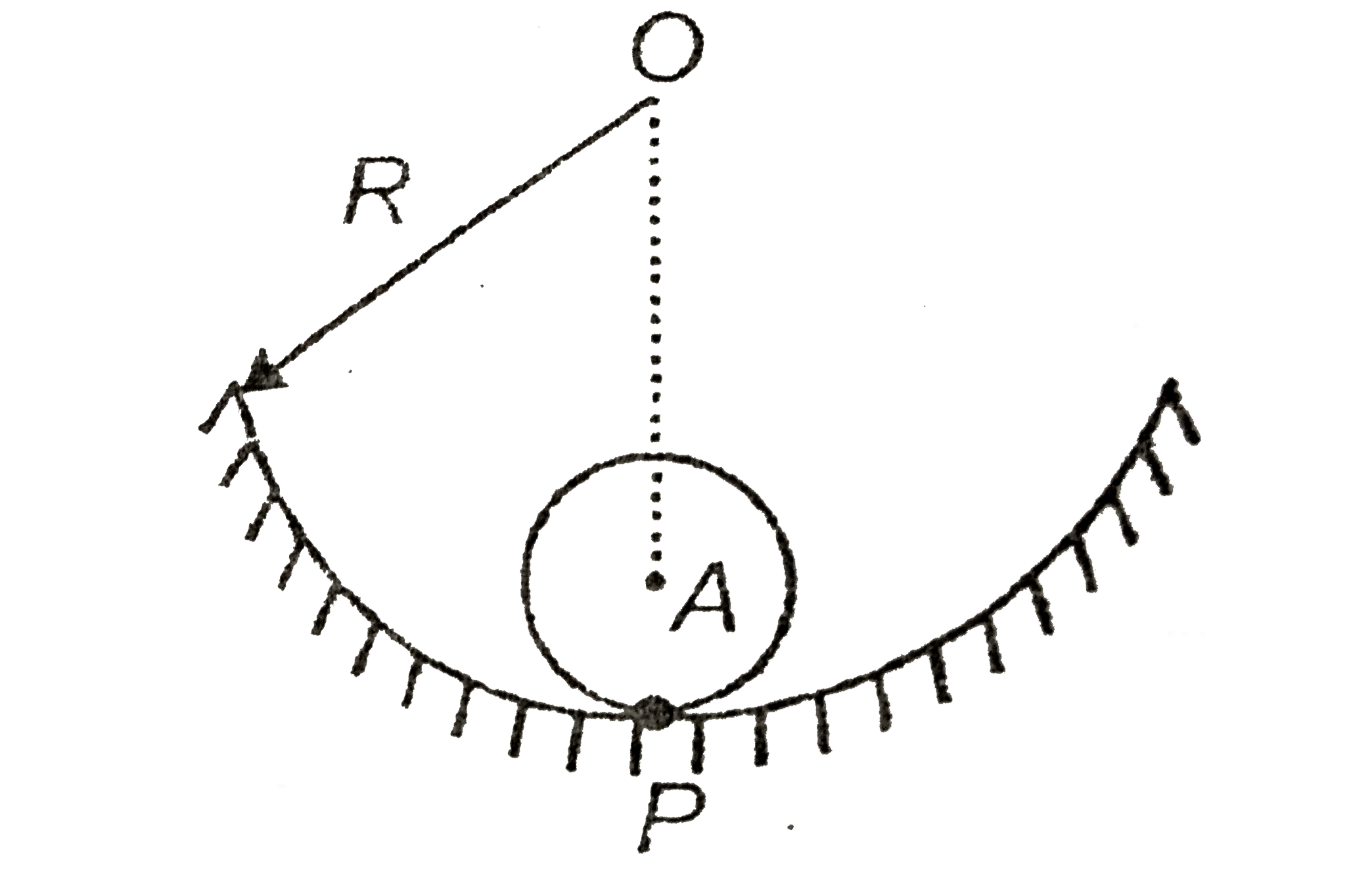
View SolutionA small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
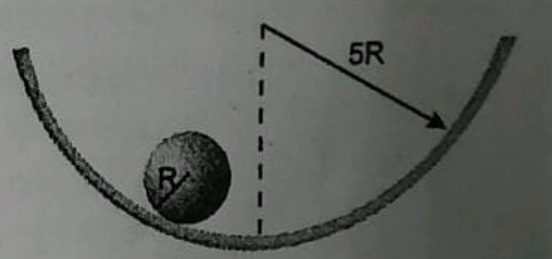
View SolutionA solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

View Solution
