Let O be an interior points of △ABC such that −−→OA+−−→OB+3→OC=→0, then the ratio of △ABC to area of △AOC is
The correct Answer is:3
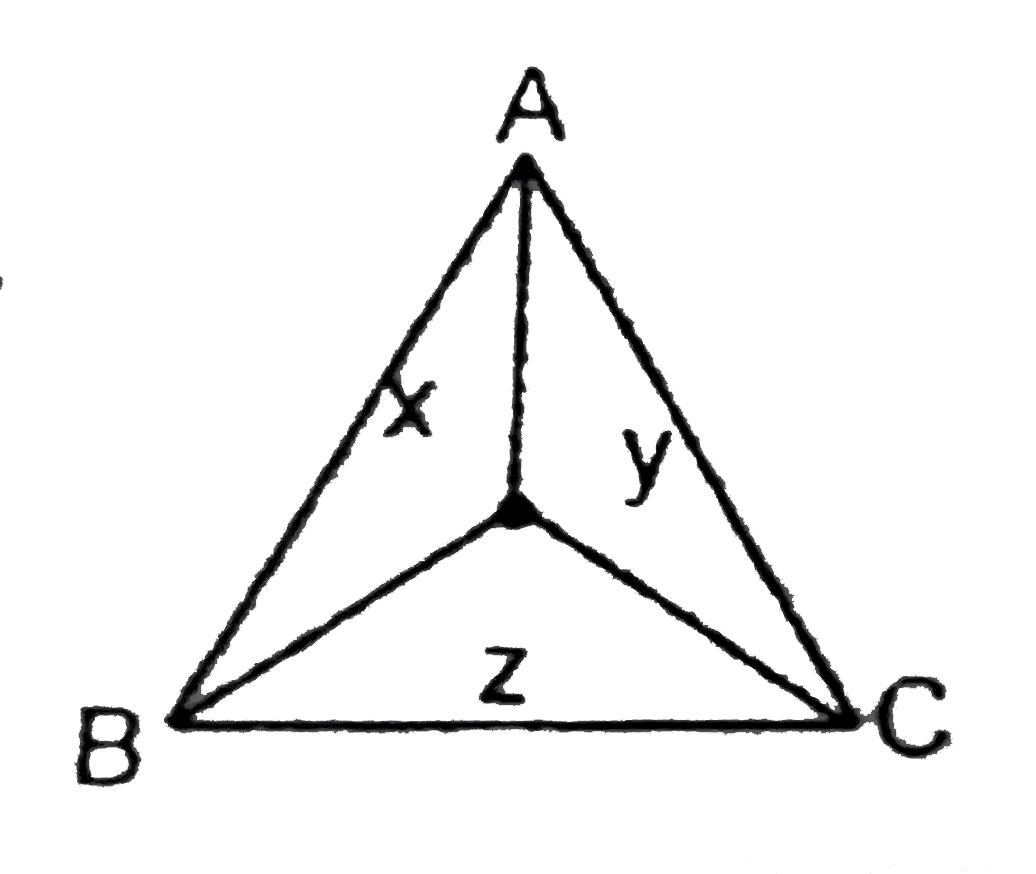
¯¯¯¯¯¯OA+¯¯¯¯¯¯¯¯2OB+¯¯¯¯¯¯¯¯3OC=ver0 .(i)
let x,y,z be the area of Delta OAB,OBC and OCA
respectively and area (ΔABC)=A
⇒x+y+z=A .(ii)
Taking cross product with ¯¯¯¯¯¯OA on the both sides (i) and then take modulus on both sides. We get
xy=32⇒x+32y
similarly xz=3 and yz=2⇒z=y2
∵ from (ii) y(32+1+12)=A⇒Ay=3
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Video
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - MATHEMATICS
48 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - MATHEMATICS
132 Videos
Similar Questions
Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
View Solutionif G is the centroid of △ABC such that −−→GBand−−→GC are inclined at on obtuse angle, then
View SolutionGiven, the angles A, B and C of △ABC. Let M be the mid-point of segment AB and let D be the foot of the bisector of ∠C. Find the ratio of AreaOf△CDMAreaof△ABC
View SolutionLet △ABC be a given triangle. If ∣∣∣−−→BA−t−−→BC∣∣∣≥∣∣∣−−→AC∣∣∣ for any t∈R,then △ABC is
View SolutionIf O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionLet →a,→b and →c be unit vectors such that →a+→b−→c=0. If the area of triangle formed by vectors →aand→b is A, then what is the value of 4A2?
View SolutionIn a triangle OAC, if B is the mid point of side AC and →OA=→a, →OB=→b, then what is →OC?
View SolutionStatement 1: let A(→i+→j+→k)andB(→i−→j+→k) be two points. Then point P(2→i+3→j+→k) lies exterior to the sphere with AB as its diameter. ,
Statement 2: If AandB are any two points and P is a point in space such that −−→PA.−−→PB>0 , then point P lies exterior to the sphere with AB as its diameter.
View Solution
