White light of wavelength in range 400 nm to 700 nm is incident normaly on a young's double slit experiment apparatus. The distance betweenn slits is d=1 mm and distance between plane of the slits and screen in 0.8 m. At a point on the screen just in front of one of the slits the missing wavelength is (are)
533.3 nm
416.7 nm
666.7 nm
577.7 nm
The correct Answer is:B
To solve the problem of finding the missing wavelength in a Young's double slit experiment with white light, we can follow these steps:
1. Understanding the Setup:
- We have a double-slit experiment where white light (wavelength range 400 nm to 700 nm) is incident normally on the slits.
- The distance between the slits d=1mm=1×10−3m.
- The distance from the slits to the screen D=0.8m.
2. Path Difference:
- The path difference Δx for light coming from the two slits to a point on the screen can be expressed as:
Δx=dsinθ
- For small angles, sinθ≈tanθ, where tanθ=yD (with y being the vertical distance from the central maximum to the point on the screen).
3. Expression for Path Difference:
- Thus, we can write:
Δx=dyD
4. Condition for Dark Fringes:
- The condition for dark fringes (missing wavelengths) is given by:
Δx=(n+12)λ
- Here, n is an integer (0, 1, 2, ...), and λ is the wavelength.
5. Equating the Two Expressions:
- Setting the two expressions for path difference equal gives:
dyD=(n+12)λ
6. Finding Wavelength:
- Rearranging gives:
λ=dyD(n+12)
7. Calculating Wavelength for Missing Values:
- Since we are looking for the missing wavelengths, we need to find λ for different values of n.
- Substitute d=1×10−3m and D=0.8m:
λ=(1×10−3)y0.8(n+12)
8. Finding Specific Values:
- For n=0:
λ=(1×10−3)y0.8×0.5=(1×10−3)y0.4=2.5×10−3y
- For n=1:
λ=(1×10−3)y0.8×1.5=(1×10−3)y1.2≈8.33×10−4y
- Continue this for n=2,3,… until the calculated wavelengths fall within the range of 400 nm to 700 nm.
9. Final Calculation:
- After calculating for different n, we find that the first missing wavelength in the range is approximately 416.67nm for n=1.
Conclusion:
The missing wavelength is approximately 416.67 nm, which falls within the visible spectrum of white light.
- We have a double-slit experiment where white light (wavelength range 400 nm to 700 nm) is incident normally on the slits.
- The distance between the slits d=1mm=1×10−3m.
- The distance from the slits to the screen D=0.8m.
- The path difference Δx for light coming from the two slits to a point on the screen can be expressed as:
Δx=dsinθ
- For small angles, sinθ≈tanθ, where tanθ=yD (with y being the vertical distance from the central maximum to the point on the screen).
- Thus, we can write:
Δx=dyD
- The condition for dark fringes (missing wavelengths) is given by:
Δx=(n+12)λ
- Here, n is an integer (0, 1, 2, ...), and λ is the wavelength.
- Setting the two expressions for path difference equal gives:
dyD=(n+12)λ
- Rearranging gives:
λ=dyD(n+12)
- Since we are looking for the missing wavelengths, we need to find λ for different values of n.
- Substitute d=1×10−3m and D=0.8m:
λ=(1×10−3)y0.8(n+12)
- For n=0:
λ=(1×10−3)y0.8×0.5=(1×10−3)y0.4=2.5×10−3y
- For n=1:
λ=(1×10−3)y0.8×1.5=(1×10−3)y1.2≈8.33×10−4y
- Continue this for n=2,3,… until the calculated wavelengths fall within the range of 400 nm to 700 nm.
- After calculating for different n, we find that the first missing wavelength in the range is approximately 416.67nm for n=1.
The missing wavelength is approximately 416.67 nm, which falls within the visible spectrum of white light.
Similar Questions
At a point on the screen directly in front of one of the slits, find the missing wavelengths.
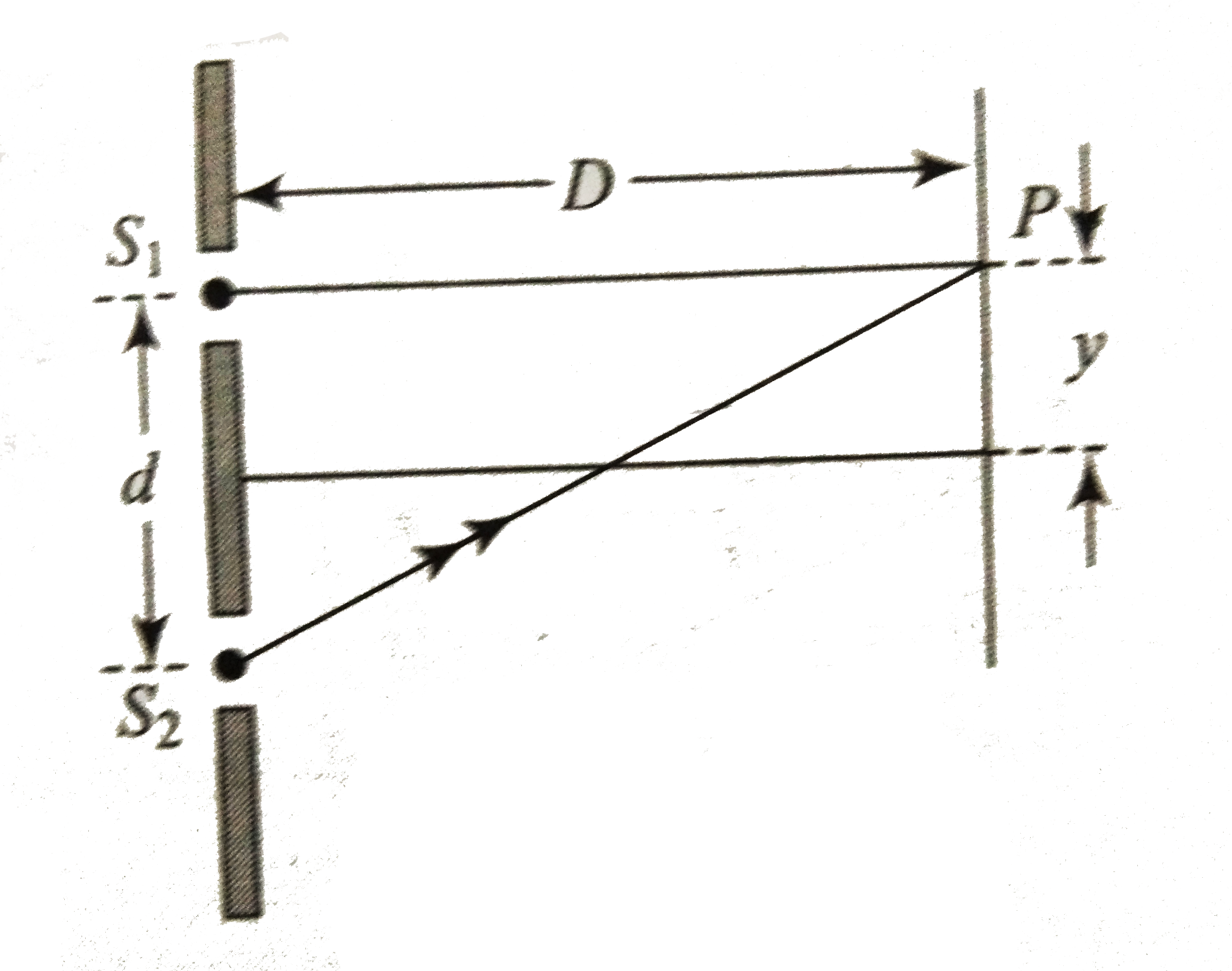
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn young's double slit experiment, distance between the slit S1andS2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S1 is
View SolutionWhite light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance d(>>b) from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionIn Young's double-slit experiment, the separation between the slits is d, distance between the slit and screen is D(D>>d), In the interference pattern, there is a maxima exactly in front of each slit. Then the possilbe wavelength(s) used in the experiment are
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View Solution

